The theory of conformational analysis

The theory is introduced with reference to trying to explain why the eclipsed form of ethane is ~2.6 kcal/mol higher in energy than the staggered conformation (this barrier was inferred by Pitzer and Kemp from trying to reproduce the correct entropy for ethane: DOI: 10.1021/ja01281a014). There are three effects which are added together:

• Effect one: Orbital overlap or bond orientation. Pitzer and Lipscomb first proposed in 1963 (DOI: 10.1063/1.1734572) that there was an attractive force favouring the anti-peri-planar (abreviated app) conformation due to a favourable alignment of the orbitals describing the C-H bonds. In 1979 Brunck and Weinhold (DOI: 10.1021/ja00501a009) derived equations for obtaining an appropriate orbital (which we now call Natural bond orbitals, or NBOs). These come in the form of a C-H bonding σ-orbital describing the pair of electrons located along the C-H covalent bond, and a C-H σ*-orbital describing the anti-bonding form of this orbital and containing no electrons.
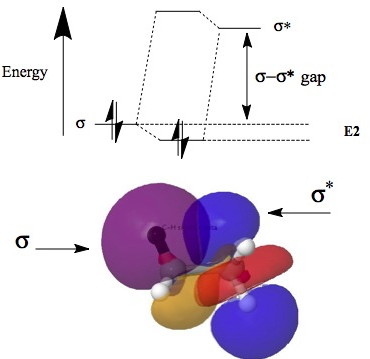
  A form of theory known as second-order perturbation theory shows how the pair of electrons in such a σ-orbital interacts with the vacant σ*-orbital orbital. The result is stabilization of the filled bonding NBO (by an energy E(2)) and destabilization (by an energy >E(2)) of the antibonding NBO. Since the latter has no electrons, the overall effect is of stabilization, but only if
  • if the σ-σ* energy gap is sufficiently small
  • the two orbitals can overlap efficiently. This overlap is optimal for the anti-periplanar orientation.

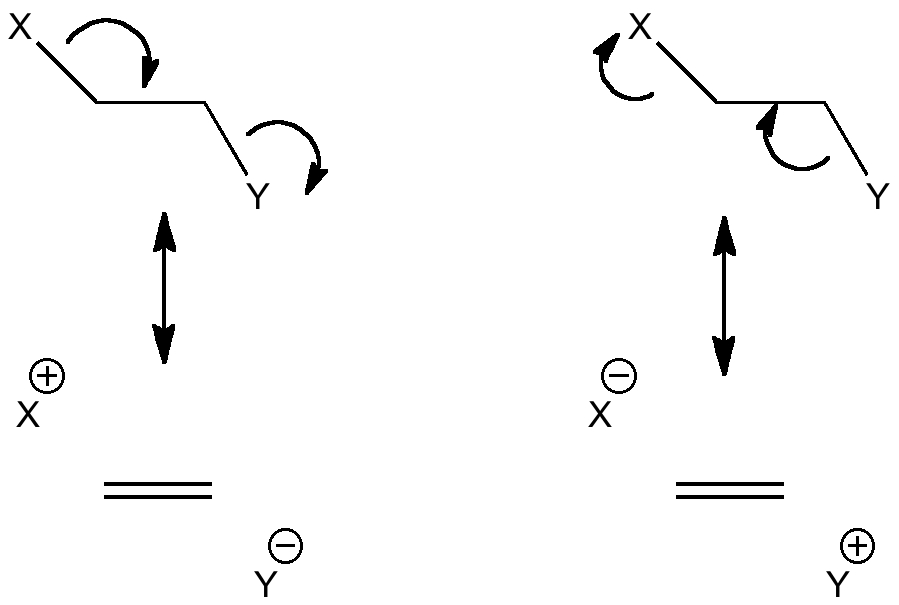
  This effect can be represented using "arrow pushing" as conjugation of the following type (X=Y=H for ethane):
  
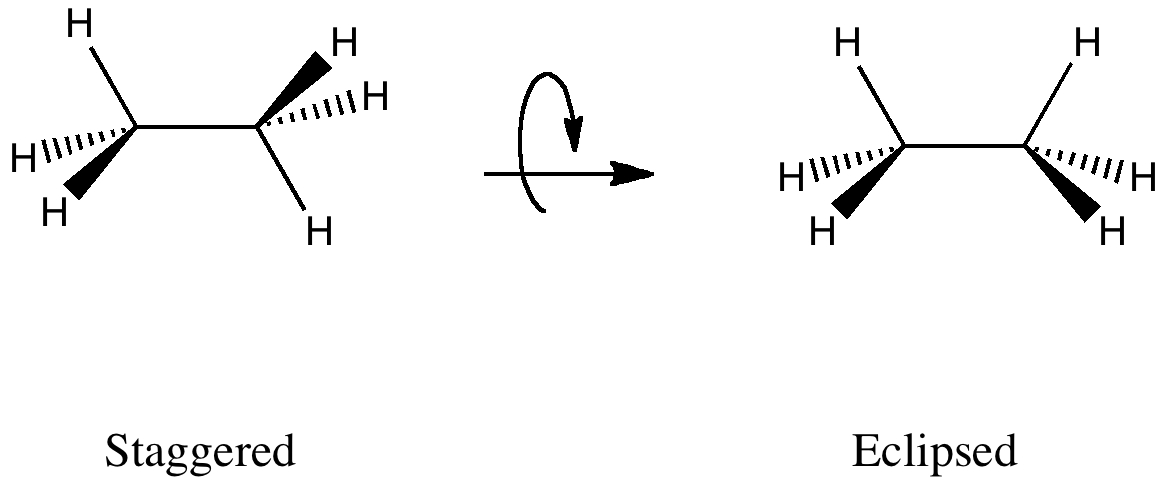
  In staggered ethane, there are six (equivalent) anti-periplanar interactions between pairs of a σ_C-H -orbital and a σ*_C-H -orbital (X=Y=H), for each of which E(2) = 3.2 kcal/mol.

  These anti-periplanar orientations are all missing in the eclipsed orientation, being replaced by syn-periplanar interactions for which E(2) has the smaller value of 1.3 kcal/mol each due to reduced overlap.

  

• ---

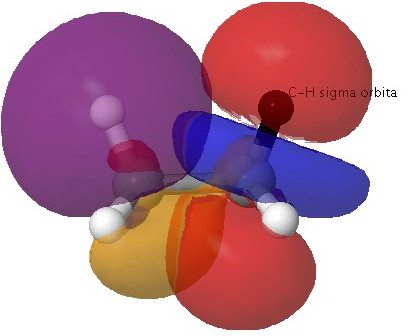
  Effect two: Bond-bond or Pauli repulsions. In a similar manner, one can show that the interaction between two occupied C-H σ-orbitals results in overall destabilization (the top orbital being destabilized by more than the bottom is stabilized).
  • Thus the total pairwise (steric) repulsions in eclipsed ethane comprise three pairs of eclipsed C-H bonds and six pairs of C-H bonds oriented at 120°; +22.3 kcal/mol (for details, see here).
  • In staggered ethane, three anti-periplanar and six C-H pairs oriented at 60° totalling +21.9 kcal/mol

  Overall, these favour the staggered form (by 0.4 kcal/mol). Whilst the effect is relatively small in ethane, as molecules get larger, it mounts up! In general however, effect one is more stabilizing than effect two is destabilizing.

  

• ---

  Effect three: van der Waals (dispersion) forces. Whereas effects 1 and 2 operate at relatively short (bonded) internuclear distances a rather different one operates at longer (non-bonded) inter-atomic distances:
  
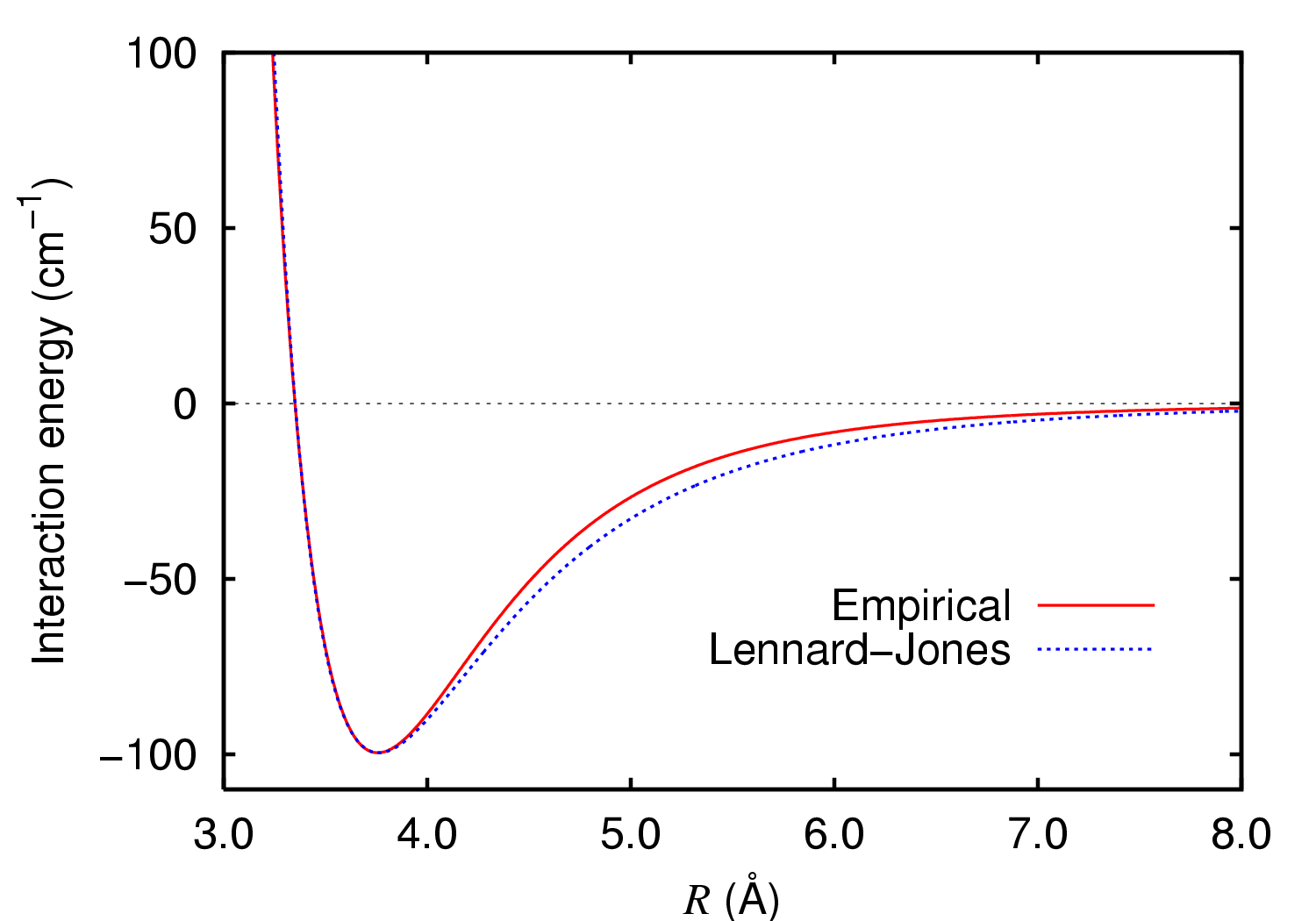
  At short distances the function is strongly repulsive (see also 2 above), but at longer distances it actually becomes attractive (which is why longer chain alkanes tend to be liquids and not gases, vis petrol!). The maximum attraction occurs at a distance corresponding to the sum of the so-called van der Waals radii for the two atoms concerned. For argon, this radius is 2*1.88Å =3.76Å (above, 100 cm^-1 ~0.3 kcal/mol or ~1.3 kJ/mol). For hydrogen, that radius is 1.2Å (when interacting with other hydrogens) or 1.1Å (when interacting with other elements, see DOI: 10.1021/jp8111556, 10.1002/chem.200800987, 10.1524/zkri.2009.1158). In typical organic compounds, this means that maximum attraction occurs at the following distances for typical pairs of non-bonded atoms:
  1. H...H; 2.4Å (becoming repulsive at ~<2.1Å unless it's a dihydrogen bond).
  2. C...H; 2.7Å
  3. N...H; 2.58Å
  4. O...H; 2.62Å
  5. Cl...H; 2.85Å
  6. F...F; 2.9Å
  7. C...C; 3.2Å
  8. Cl...Cl; 3.5Å
  9. Br...Br; 3.9Å
  10. "Me"..."Me"; 4.0Å
  11. I...I; 4.3Å

Od Hassel (in 1943) and Derek Barton (in 1948, DOI: 10.1039/JR9480000340) followed Bill Penney (1934) in recognising "The significance of van der Waals atomic radii for the stereochemical structure of molecules". Hassel and Barton won the Nobel prize in 1969. Remember also that whilst the interaction energy for any two atoms is relatively small (~1 kJ = 0.3 kcal/mol), the total number of such interactions goes up very rapidly for larger molecules (and it can be very large indeed for molecules the size of e.g. proteins). For ethane, the difference in van der Waals/dispersion attractions for the two orientations of ethane is tiny (~0.05 kcal/mol) but again the effect grows strongly with the size of the molecule.

For wonderfully detailed, but still readable explanations of what goes on at the surface of a gecko's foot, see 10.1002/adfm.201100493. or on the topic of bio-inspired adhesives: 10.1002/adfm.201100982. The other famous example of how attractive dispersion forces can be is the difficulty in pulling apart two telephone directories.

There is a crucial difference between the three effects. Effects 1 and 2 are highly directional (anisotropic) whereas effect 3 is isotropic, which means it depends only on the distance between two non-bonded atoms and not on their relative orientation.

Summary of important concepts

1. Conformational processes are dynamic and the thermodynamic equilibrium population of conformers about the C-C bonds is determined by:
   • maximising σ_C-H/σ*_C-H and/or σ_C-C/σ*_C-C conjugation
   • minimising σ_C-H/σ_C-H and/or σ_C-C/σ_C-C bond electron repulsion (Pauli repulsion)
   • optimising van der Waals (dispersion) interactions between non-bonded atom pairs

© Henry S. Rzepa, 2010-2014. Hide|show Toolbar.