Cycloalkanes
Rings, and particularly cyclohexane, is where conformational analysis started. We will deal here only with ring sizes 3-6 initially, and return to larger ones later.
Cyclopropane

The ring structure of cyclopropanes is necessarily flat. It is actually quite a common motif, and occurs in many natural products. This shape confers torsional strain along each of its C-C bonds because the substituents, which project above and below the plane of the ring, cannot avoid being eclipsed. Because of this eclipsed nature of the bonds, the σ resonance is rather lower (σC-H/σ*C-H E2 1.5 kcal/mol) than that found for ethane.
Cyclobutane
Cyclobutanes may deviate slightly from the planar conformation and thereby switch to one which is called the puckered conformation

In the puckered conformation substituents on vicinal carbons are twisted slightly out of the eclipsed arrangement thereby relieving the torsional strain somewhat. However the puckering process can only be taken so far before the distance between the two R groups enters the repulsive van der Waals region.

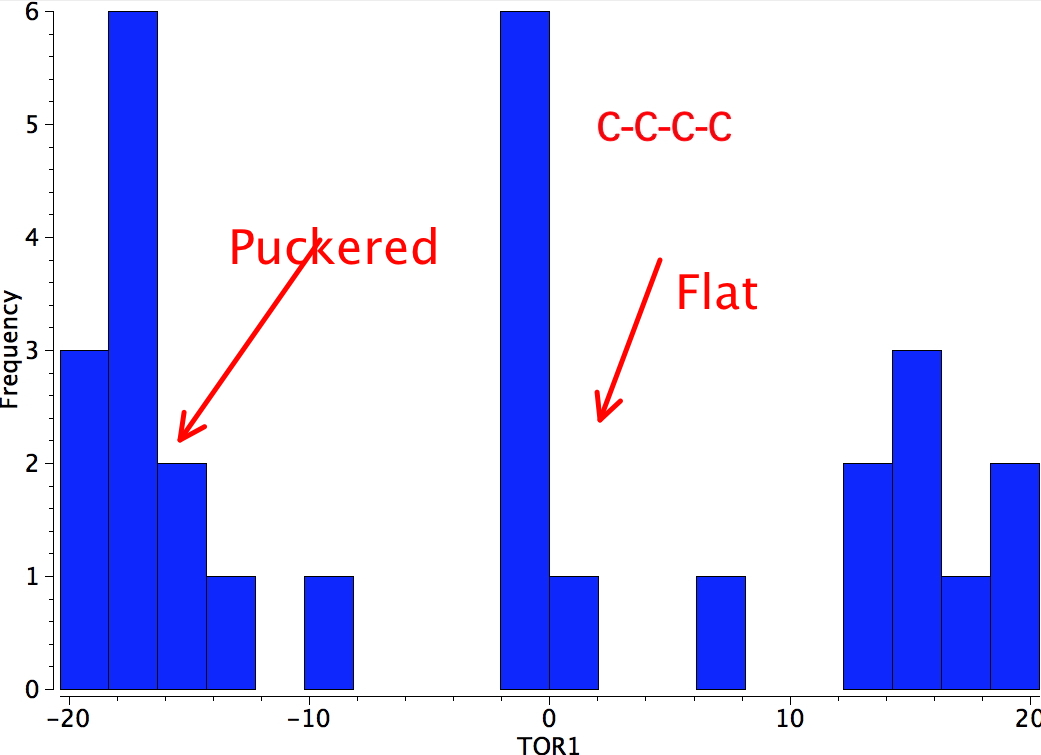
The energy difference between the planar and puckered conformations of many cyclobutanes is not large (<1 kcal/mol) and it is often difficult to decide simply by inspection which conformation will be adopted.
Thus, the trans-1,3-dicarboxylic acid has a planar arrangement in the solid state (by X-ray analysis)
and the puckered state in aqueous solution (by the lack of symmetry indicated by Raman and IR studies). Its dianion is however planar in solution.
In contrast the cis-1,3-dicarboxylic acid is puckered in the solid state. Trans-1,3-dibromoderivative is also puckered since it shows a dipole moment of 1.10D which corresponds to a puckering angle of 143°.

Cyclopentane
Along with cyclohexane, this motif is the most common saturated ring system. To study its conformational preferences, we will adopt a new technique. This involves optimising the geometry of the ring with the constraint that all the ring carbon atoms are restricted to co-planarity. This geometry is then subjected to a vibrational analysis, and the result normal vibrational modes (3N-6 of them) are inspected to see if any of the force constants they derive from are negative. If one force constant is computed negative, then we have found a transition state, and this in fact was the case for cyclobutane above.

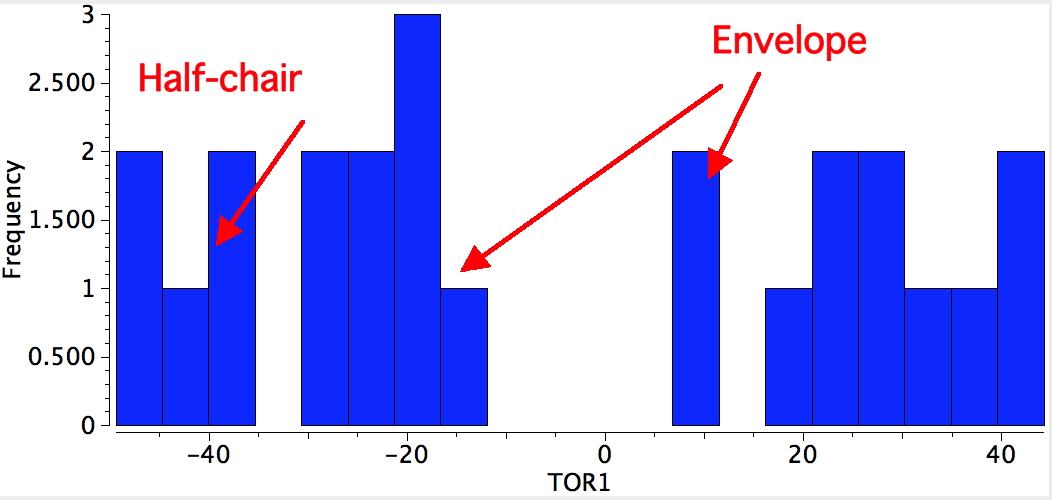
In the case of cyclopentane, two negative force constants are computed. This means that the planar geometry has precisely two ways of distorting to reduce the energy of the system. The eigenvectors corresponding to each of these force constants can be displayed as a twist or as a buckle resulting in more or less two isoenergetic conformations which have respectively a C2 axis of symmetry (also called a half-chair) and a Cs plane of symmetry (also called an envelope). Neither achieves full staggering of the C-H bonds, nor do the C-C-C angles achieve the ideal 109.47° angle, so each is a compromise.
The half-chair conformation has the distinction of being almost the smallest organic compound to exhibit chirality (αD = 13.6°), although the barrier to enantiomerisation is so small that it is impossible to prevent at normal temperatures (the smallest is probably the isopropyl cation mentioned in the previous lecture).
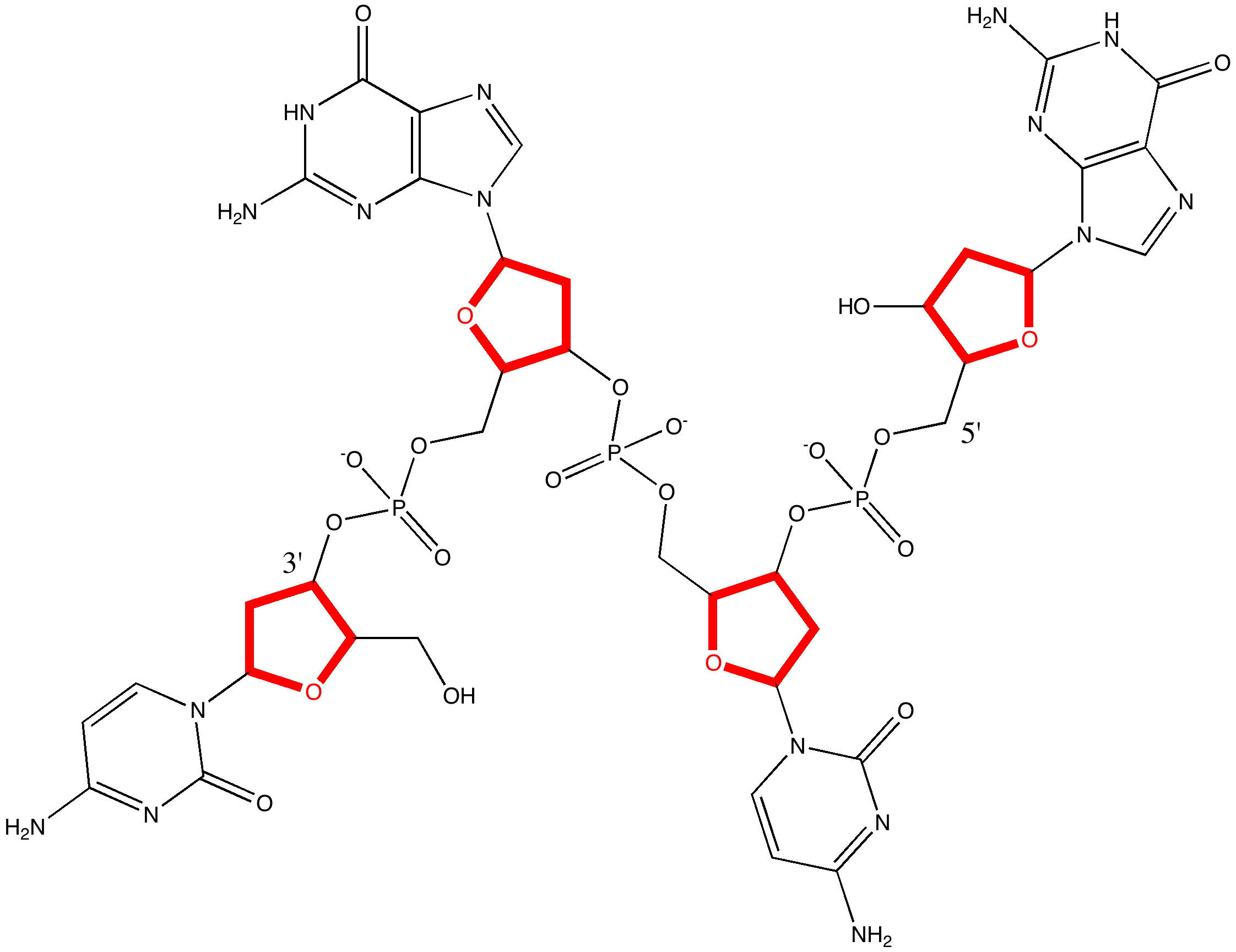
Five membered rings have another distinction, featuring in the ribose sugar unit in DNA and RNA. The envelope conformation adopted by this ring is critical in understanding the conformation adopted by DNA itself (which features three important conformations itself, comprising a combination of that for the ribose and that of the helix itself, and which are known as A-DNA, B-DNA and Z-DNA).
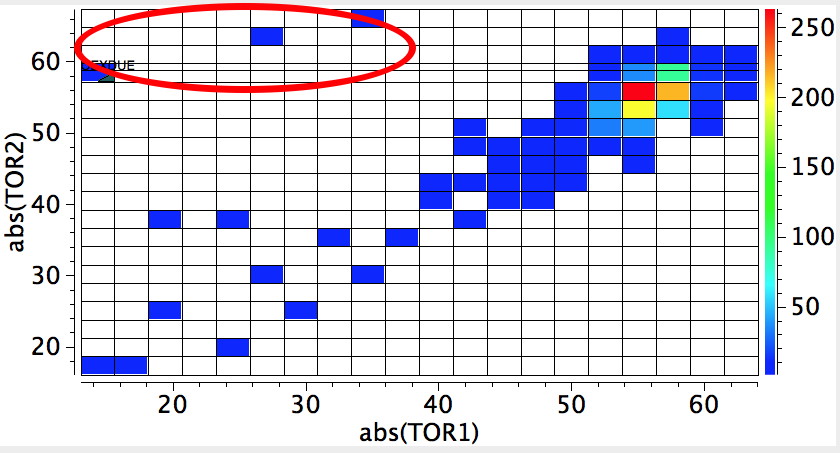
 This is where the conformational analysis story started, and since its an enormous topic, we can only cover a tiny fraction of what is known here. Let us start in the same manner as cyclopentane, namely calculate the force constants for planar cyclohexane. This time, three negative force constants are computed, each leading to a chair, a twist boat and boat.
This is where the conformational analysis story started, and since its an enormous topic, we can only cover a tiny fraction of what is known here. Let us start in the same manner as cyclopentane, namely calculate the force constants for planar cyclohexane. This time, three negative force constants are computed, each leading to a chair, a twist boat and boat.
Something odd happens with the boat, since it too has one negative force constant (the first two have none), and it turns out that the vectors of this force constant correspond to the transition state for enantiomerisation of the twist-boat structure (which is again chiral, (αD = 38°). Cyclohexane then has only three conformations, the chair and two (enantiomeric) twist-boats (only the latter being chiral). Historically, the first investigation of the interconversion between these chair and boat forms was as far back as 1938 (DOI: 10.1021/ja01277a020).
The experimental determination of the relative energy of the twist-boat form compared to the chair form was made in 1975 (DOI: 10.1021/ja00844a068). Cyclohexane vapour at 1000K, which contains a much higher proportion (~30%) of the twist boat form than is present at room temperature (~0.1%), was rapidly cooled and condensed onto a CsI plate held at 20K. An infra-red spectrum of this cold-trapped cyclohexane indicated extra bands due to the twist-boat form compared to a sample cold-trapped from room temperature which only shows bands due to the chair form. By looking at the rates of loss of these extra bands, the separate rates of conversion of the twist-boat form to the chair form at temperatures between 72.5K and 74K could be determined and the fairly accurate estimate of the energy, above, of the twist-boat form was made from that data, it being around 5 kcal/mol higher than the chair at room temperatures.
The crystal structure of pure cyclohexane has now been determined and it indeed confirms the chair form. It also has one other remarkable property, which often causes confusion in laboratories; a melting point of 6.5°C (it crystallises in ice, and this crystallisation can be the source of much confusion). The origin of this unexpectedly high melting point (for an alkane) might be the attractive H...H contacts (of ~2.5Å) possible in the crystal structure, which cummulatively could serve to make the lattice quite rigid (but the case is not entirely convincing).
Starting with this chair conformation, we note that the twelve hydrogen atoms in cyclohexane form a set of six which are axially oriented, and another set of six which we call equatorial. We know however that at room temperatures, cyclohexane exhibits only a single sharp 1H NMR resonance for all twelve hydrogens. Of course, this process may be slowed down at low temperatures and when sufficiently cold (~203K, see DOI: 10.1021/ja9714898) two lines appear in the 1H NMR spectrum of cyclohexane-d11

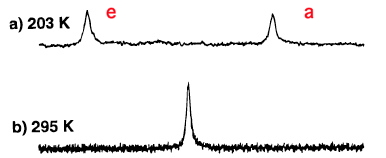
It took a few years to work out how the two sets of hydrogens interconvert with each other:
- Starting with one form of the chair
- one of the CH2 groups starts a twist motion to reach a transition state called the twisted half-chair (and in the process of twisting, becomes chiral),
- and then drops down to reach one enantiomer of a twist boat.
- The momentum of the previous step carries the system to a further twist leading to a boat transition state which represents the half way point of the journey. This has a mirror plane of symmetry (and so is not chiral).
- The second half of the motion is in effect the mirror image of the first, at the end of which the two sets of hydrogen atoms have exchanged their environments. The high-energy point of this journey (the twisted half-chair transition state) represents passage over a free-energy barrier of ~10 kcal/mol.

This process can be summarised by

Since most cyclohexanes exist in the chair form rather than the much higher energy twist-boat form (for a rare example of the latter, see here) conformational analysis is almost exclusively applied to substituents on cyclohexanes in the chair conformation and this conformation will form the mainstay of our discussions.
Methyl and t-Butyl Cyclohexane
When cyclohexane is mono-substituted, the substituent can occupy either the axial or the equatorial position. In fact almost all known such substituents occupy the latter,
although the reasons are due to all three factors discussed in previous lecture.
- σC-C/σ*C-C, σC-H/σ*C-C and σC-H/σ*C-H anti-periplanar conjugations all tend to favour the equatorial over the axial conformation. Thus for methylcyclohexane, there are four app sets of these conjugations at the substituted carbon, which sum to 12.9 kcal/mol for methyl equatorial, and 12.2 for methyl axial.
- the van der Waals (dispersion) attractions on the other hand favour axial, by 0.5 kcal/mol.
- the bond electron (Pauli) repulsions adjudicate in final favour of the equatorial form by 1.8 kcal/mol. The experimentally measured difference for methyl cyclohexane is ~1.7 kcal/mol.
This value arises mostly from filled pair repulsions involving the parallel 1,3,5-C-H/C-Me bonds, which are absent in the equatorial form and which are referred to as 1,3-diaxial compression.

- One can also regard the axial conformation as having TWO C-X (X=Me) gauche orientations with the adjacent C-C bonds (blue), whereas these are both antiperiplanar
in equatorial conformation (red), and hence the axial form is disfavoured for the same reason that e.g. gauche butane is.
For a substituent X=tButyl, the 1,3 diaxial repulsions and other geometric distorsions result in a greater energy
difference; 5.9 kcal/mol, which when used in the expression ΔG = -RTLnK, indicates K >20,000 in favour of the rhs.
This indicates that this large substituent effectively locks the equilibrium into a single conformation
(see this crystal structure and also doi: 10.1021/jp0550311).
When t-butyl and iodine are placed into competition, the t-butyl wins!.
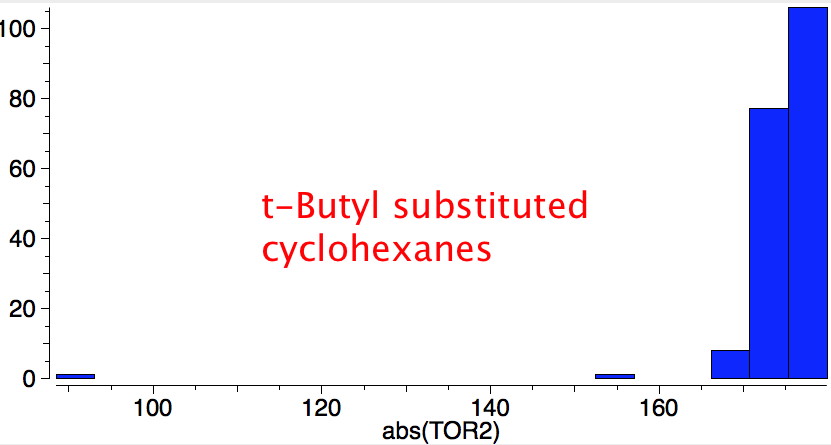
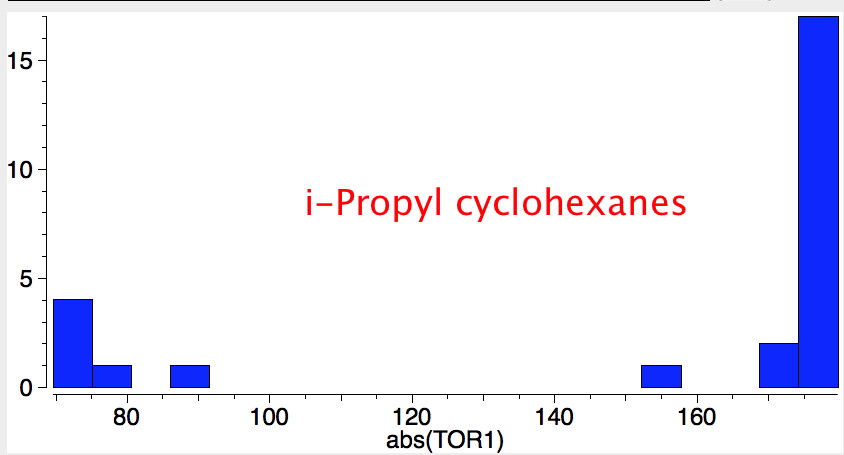
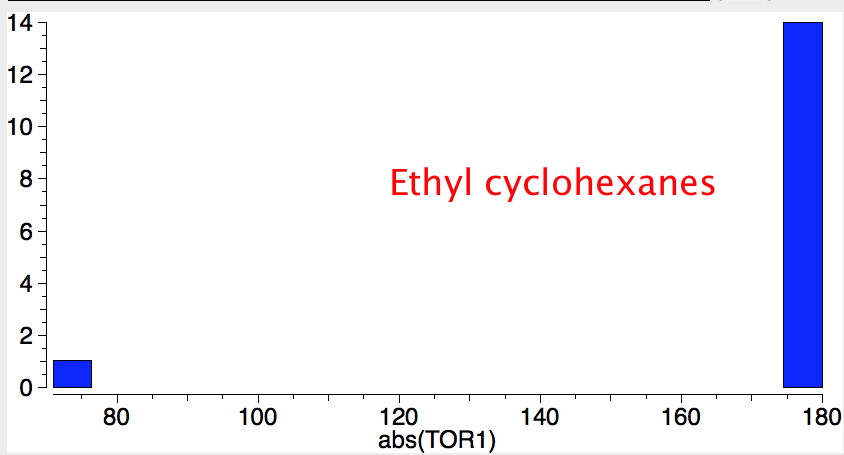
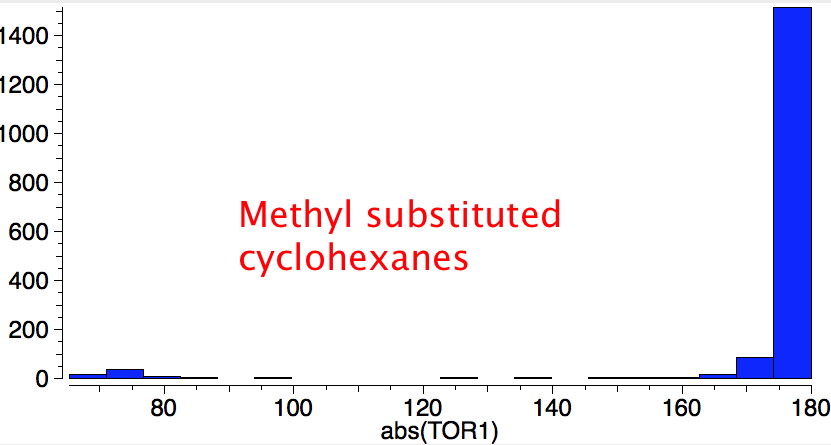
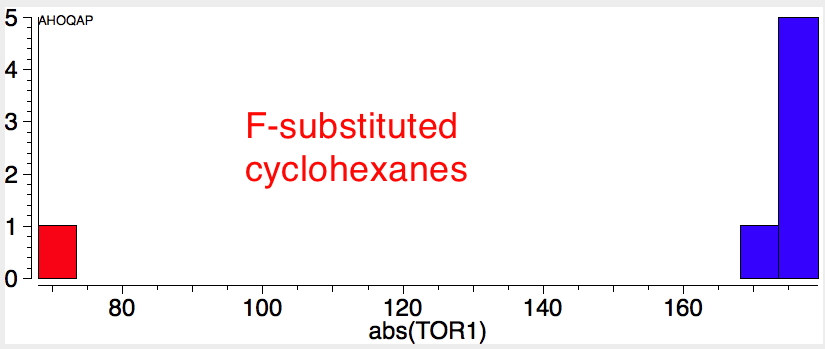
Reactions of cyclohexanes
Earlier, we saw how anti-periplanar alignment of a donor bond orbital with an acceptor antibond orbital could explain conformational preferences in heteroalkanes. Exactly the same principle applies to a transition state of a reaction, except that the effect is actually much larger than for equilibrium geometries. The fixed anti-periplanar relationships shown below can be exploited:
- in e.g. E2 elimination reactions: X=H (donor bond) Y=Cl (acceptor bond) shown in red
- ring contraction (or expansion) reactions: X=OH (donor lone pair/donor bond), Y=OTs (acceptor bond) shown in blue.
- A tutorial problem which explores this topic with a worked example is available
 A blog on the competition between an E2 elimination and an alternative ring contraction starting from a 1,2-dichlorocyclohexane in which one chlorine is axial (and eliminates) and the other is equatorial (and induces ring contraction).
A blog on the competition between an E2 elimination and an alternative ring contraction starting from a 1,2-dichlorocyclohexane in which one chlorine is axial (and eliminates) and the other is equatorial (and induces ring contraction).

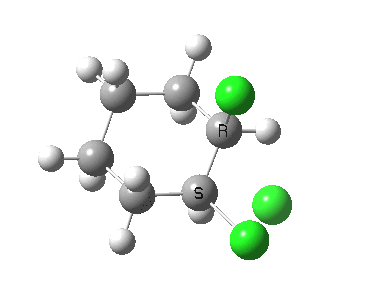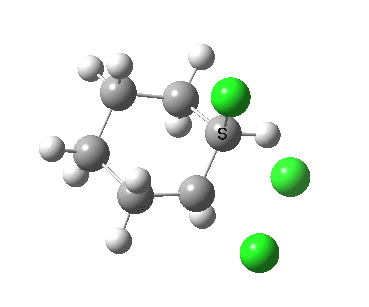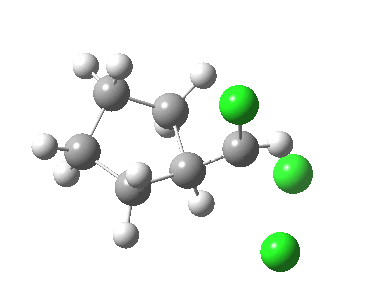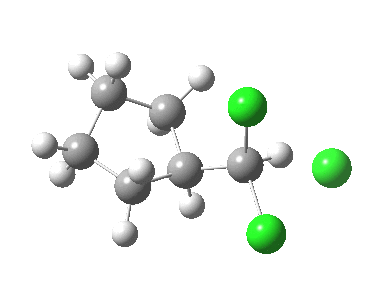
There is a vast body of chemistry dealing with both other substituents, and multiply substituted cyclohexane rings most of which is beyond the scope of the present lectures. Only two examples are noted here:
- trans 1,2,3,4,5,6-hexa-isopropylcyclohexane can potentially ring-flip so that all six isopropyl groups are either all axial or all equatorial. You might imagine (from the above results for a single tButyl) that an all-equatorial conformation would always be far lower than the all-axial. But the crystal structure (DOI: 10.1021/ja00181a036) shows that its the latter which exists in preference to the former!
- If the group is slightly smaller (ethyl) it now prefers a hexa-equatorial conformation.
The lesson we learn here is that when two large groups are on adjacent atoms in the cyclohexane ring, the di-equatorial conformation can result in increased steric repulsions between the two groups. Under these circumstances, the ring may flip to a di-axial conformation, where the two large groups are now as far apart as they can be (for an example see here), but where each of these groups now encounters more 1,3-diaxial compressions themselves. This can all be summarised as follows:
- The larger of the two substituents at any ring carbon will favour the equatorial position.
- Two large groups in a 1,3 di-axial orientation is not favoured.
- If two large groups are on adjacent ring carbons, the balance between di-equatorial and di-axial, or the balance between axial-equatorial and equatorial-axial may be quite even, depending of course on the size of the groups.
- As more large groups (iPr or larger) occur on adjacent ring positions, axial orientations gradually become favoured, until with hexa-substitution, an all axial orientation dominates.
- A tutorial problem illustrating these aspects is available here.
Decalins
Another way of locking a cyclohexane ring is to fuse it with a second such ring, to form a ring system known as decalin.

In trans-fused decalin, the two rings are merged using equatorial bonds, and this now prevents either of the two chair conformations of ring A or ring B from flipping, or swapping the axial/equatorial substituents. This locked conformation can again be exploited in reactions. In the diagram below, starting from assigning the two ring junction substituents as axial, the rest of the two rings can be inferred. Thus all the substituent bonds shown in red are axial and are anti-periplanar with respect to each other. This allows e.g. elimination reactions (which require an anti-periplanar relationship) to occur using such substituents. The ring bonds themselves also inherit anti-periplanar relationships (two examples of which are shown in blue or magenta) and these can be used for migration/ring contraction/elimination reactions involving the rings themselves.


By discovering 100s of examples in the very large area of steroid chemistry (rings A and B above are the first of four rings in steroids), and classifying them according to the rules above, Barton created the area of conformational analysis, and in the process won the Nobel prize.

Homo-DNA
The conformational property of five-membered-ring pentoses in the structure of DNA was noted above. It is a curiosity that analogous six-membered-ring hexoses do not promote strong helicity in homo-DNA (DOI: 10.1021/ja062548x), it is thought because they are TOO rigid. As with the C=N character of a peptide bond, we see again that life is amazingly finely balanced! Without a way of folding DNA efficiently into a duplex (and the helix is very efficient), there would be no replication mechanism!
Summary of important Concepts
- Cyclopropanes are flat
- Cyclobutanes may avoid some of this strain by adopting a puckered conformation
- Cyclopentane has two common conformations, a chiral twisted form with C2 symmetry and an envelope with Cs symmetry.
- Cyclohexane has three conformations, prefering a chair conformation over (two enantiomeric) higher energy twist-boat forms.
- The axial/equatorial positions in chair cyclohexanes equilibrate through the (chiral) twist-boat conformation (ring flipping)
- The substituent in monosubstituted cyclohexanes adopts adopts an equatorial position over the alternative axial position
- When large groups are on adjacent carbons in a cyclohexane, the preference of di-axial/di-equatorial or axial-equatorial/equatorial-axial depends on the size of the group.
- Conformations without 1,3-Diaxial compression are favoured.
- Ring flipping is prevented in trans-decalin or inhibited in t-butyl cyclohexane derivatives
- In conformationally locked cyclohexanes and decalins, anti-periplanar relationships are key to understanding their reactions such as E2 elimination, ring contraction or expansion.
© Henry S. Rzepa, 2010-2014. Hide|show Toolbar.
 This is where the conformational analysis story started, and since its an enormous topic, we can only cover a tiny fraction of what is known here. Let us start in the same manner as cyclopentane, namely calculate the force constants for planar cyclohexane. This time, three negative force constants are computed, each leading to a chair, a twist boat and boat.
This is where the conformational analysis story started, and since its an enormous topic, we can only cover a tiny fraction of what is known here. Let us start in the same manner as cyclopentane, namely calculate the force constants for planar cyclohexane. This time, three negative force constants are computed, each leading to a chair, a twist boat and boat.