One derivative of cyclohexane with great biological significance is oxa-cyclohexane, better known as a tetrahydropyran, one (hydroxy) derivative of which is of course D-glucose (a pyranose). As one might expect, the tetrahydropyran ring adopts a chair conformation and is largely similar to cyclohexane; thus the energy barrier for ring flipping is about 10 kcal/mol in each case.
There is, however, one major effect which is much stronger in tetrahydropyrans than in cyclohexanes, and is induced by the presence of oxygen lone pairs which replace some C-H bonds. Historically this effect was seen first in sugars and hence our discussion will start from them. D-Glucose is a hemiacetal and exists in equilibrium with its open-chain aldehydic form. Closure to the ring form from the latter leads to two diastereoisomers at the hemiacetal carbon, which are called Anomers. The one with the resultant hydroxyl group up is designated the β-anomer whereas the one with the hydroxyl group down is called the α-anomer:
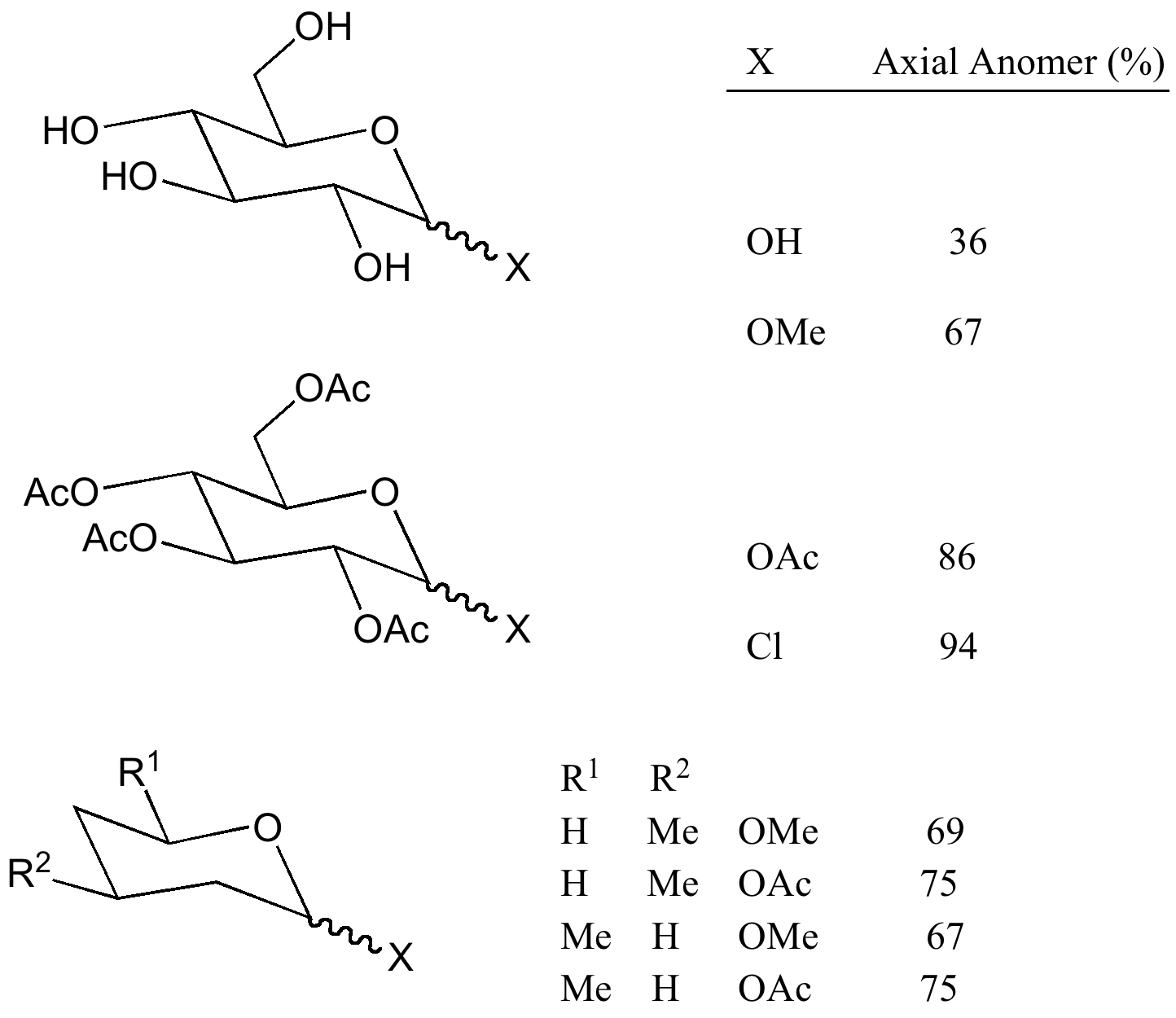
In conformational terms the β-anomer may have all the groups equatorial in one chair conformation and all of them axial in the alternative ring-flipped chair conformation. However (as with a t-butyl substituent), the former prevails by a big margin (the difference in free energy is approximately 5 kcal/mol, i.e. ~ 10000 : 1) and ring flipping is again essentially suppressed. In the α-anomer all the groups are equatorial except the anomeric hydroxyl which is now axial. At equilibrium in water the β-anomer dominates, an effect which is thought to be induced by solvation and hydrogen bonding (the equatorial anomer has a ~2D dipole moment, the axial one is close to zero). For a recent exploration of the conformation of such molecules, see doi: 10.1021/ja312393m.
However, when the anomeric substituent cannot hydrogen bond (e.g. OMe rather than OH), the α anomer clearly dominates as it is also predicted to do in non-polar or non-hydrogen bonding solvents.
We have seen the origins of this exial preference previously, as resulting from σLpO/σ*C-X conjugation. Lone pairs are less tightly bound than the electrons in a C-H bond, therefore higher in energy, leading to a smaller σLpO/σ*C-X energy gap and a larger E2 (16.3 kcal/mol in this example, X=OR).
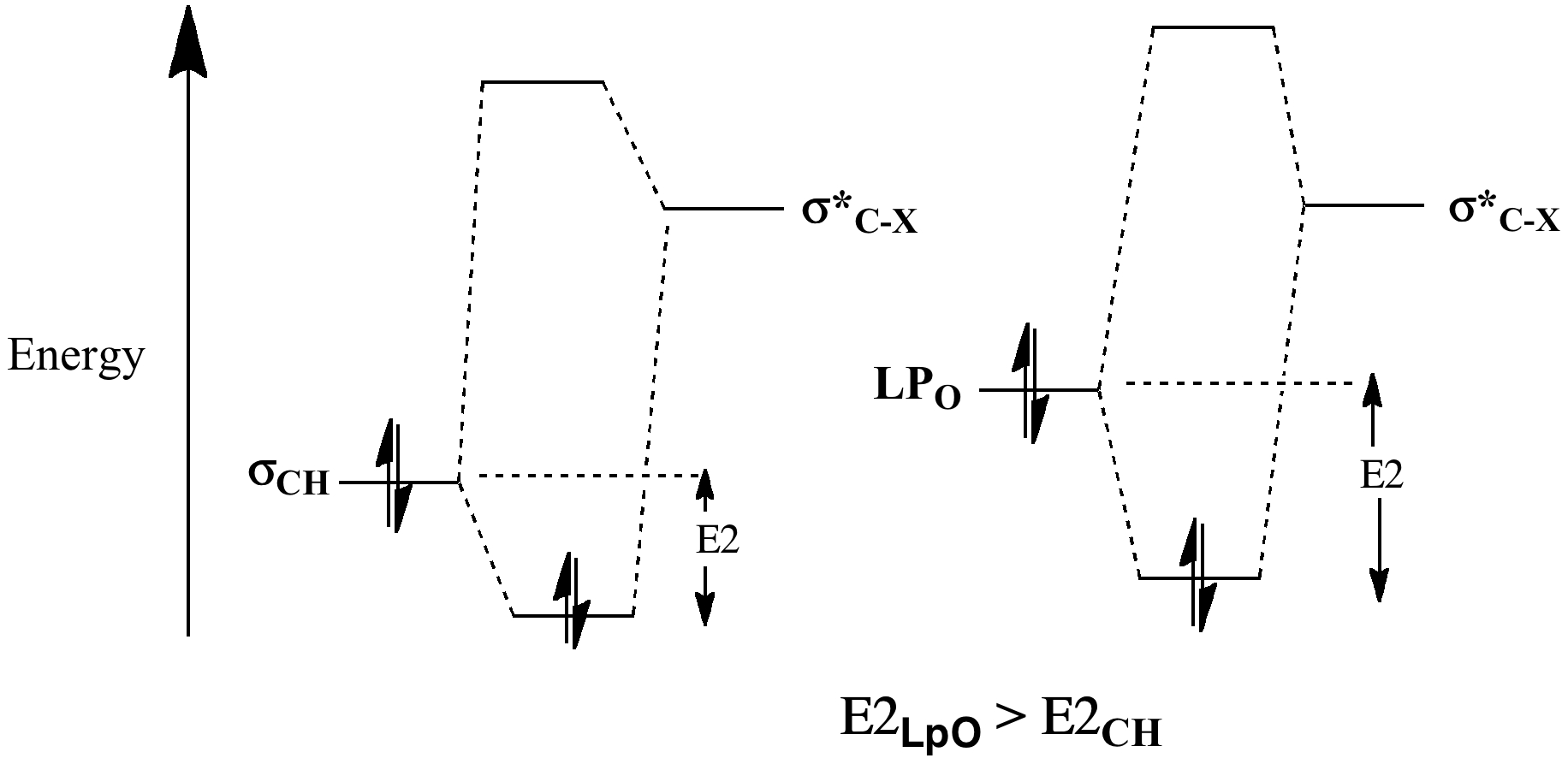
For the β-anomer, only one such interaction can be set up (red; E2 18.1 (app) and the much smaller 5.4 kcal/mol (sp)); for the α-anomer, two app interactions are now possible (red and blue; E2 16.3 and 16.3 kcal/mol, both app) including the ring oxygen, which explains the α-dominance in non-hydrogen bonded systems. In arrow pushing terms, this corresponds to the resonance/conjugation shown above. If either lone pair (on O or X) is aligned anti-periplanar (app) with the adjacent C-O/C-X bond, the conjugation will be strong. If it is not aligned, it will be weak.
In this next example, there are two app alignments (blue and red in above diagram), which need not be equal. Thus when X=Cl, the LPO/σ*C-Cl (blue arrows above, click here for actual orbitals) E2 is 25 kcal/mol. Putting electrons in the σ*C-Cl orbital lengthens the C-Cl bond (blue arrows above, blue bond below). The alternative arrow pushing LPCl/σ*C-O (red arrows above) is smaller: E2 = 10.3 kcal/mol. Overall therefore the C-Cl bond (blue bond below) in this example is lengthened more than it is contracted.
If an equatorial chlorine is added as shown above (red bond), there is no anti-periplanar LPO/σ*C-Cl alignment, only gauche. However, the alternative LPCl/σ*C-O alignment IS antiperiplanar, E2 11.3 kcal/mol which means the red C-Cl bond is now shortened rather than lengthened.
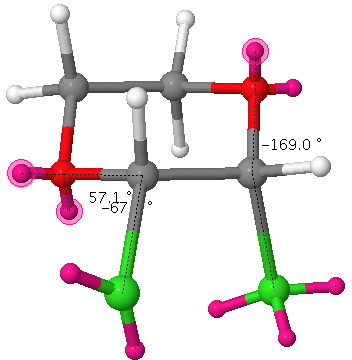
The result is that for this dichloropyran, the two C-Cl bond lengths in this molecule become distinctly different, one lengthened (blue) one shortened (red). Likewise, the two C-O distances also become different and these effects are confirmed by an X-ray structure. This variation in anti-periplanar alignments/conjugation in sugars is what makes their chemistry both complex and interesting.
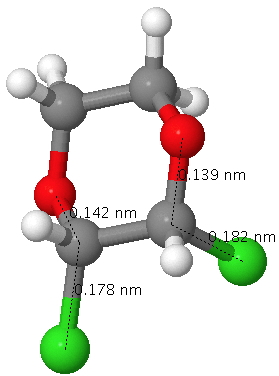
Conformational analysis can also be applied to inorganic ring systems. For example, the very involatile cyclotriborazane B/N ring system is isoelectronic with cyclohexane, and it too adopts a chair conformation (from X-ray analysis). The red hydrogens stack above the blue hydrogens in the crystal lattice forming dihydrogen bonds and making for a very rigid and hence high melting solid.
In 2013, the full conformational analysis of a pyranose monosaccharide was completed. This involved a full rotamer scan of 38 different puckering ring conformations, resulting in a total of 27,702 conformations! You can read about it at DOI: 10.1021/ja410264d
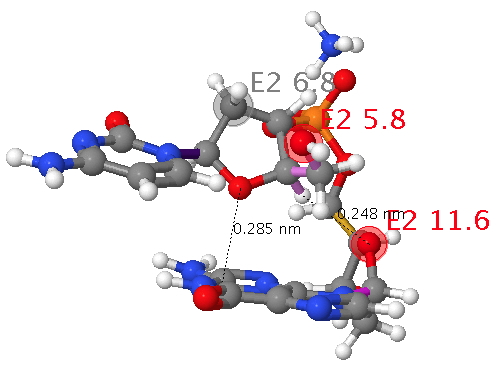
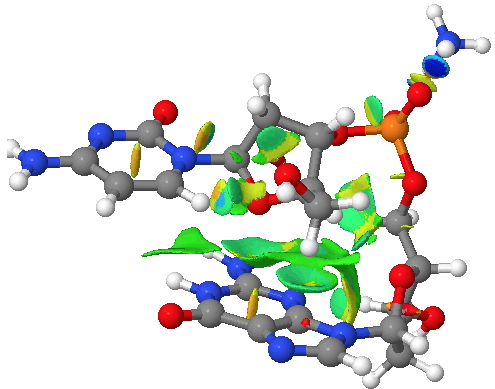
The classic heterocycloalkane is the ribose ring in DNA. This system exhibits a number of (interdependent) effects we have been discussing in this course:
© Henry S. Rzepa, 2010-2014. Hide|show Toolbar.