Four-coordinate carbon normally adopts a tetrahedral shape, where the four angles at the carbon are all 109.47°. But how large can that angle get, and can it even get to be 180°?
A search of the CSD (crystal structure database) reveals a spiropentane as having the largest such angle, VAJHAP with 164°[1]
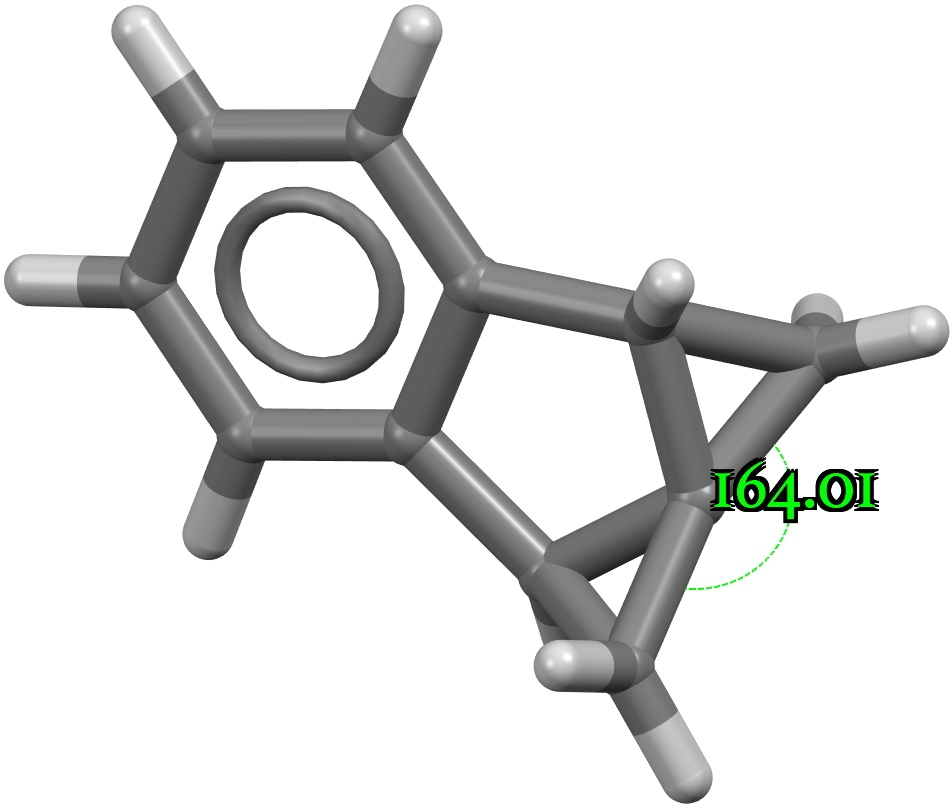
Because crystal structures might have artefacts such as disorder etc, it is always good to check this with a calculation; hence ωB97XD/Def2-TZVPP (FAIR data DOI: 10.14469/hpc/11148) for which a calculated angle of 163.8° is reassuring. The smallest angle in this system by the way is 58°, pretty normal for three-membered rings.
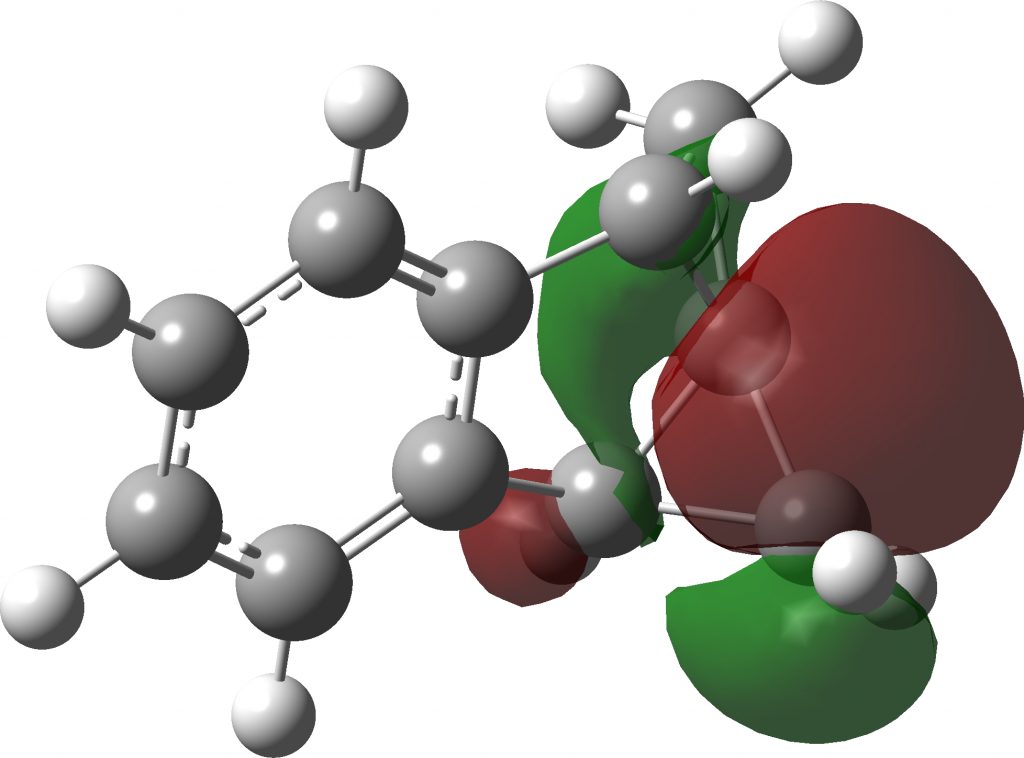
The localised orbitals show the C-C region defining the large angle to be very “bent” (a banana bond) but otherwise fairly normal.
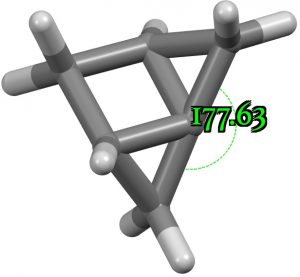
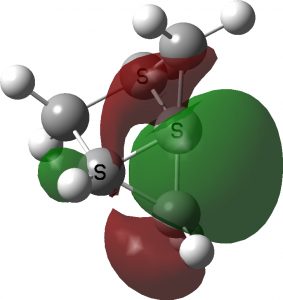
So can one “engineer” an even larger angle? Replacing the C=C of the benzo group with a shorter CH2 group produces the following, which is now almost linear (almost a “hemispherical” carbon).
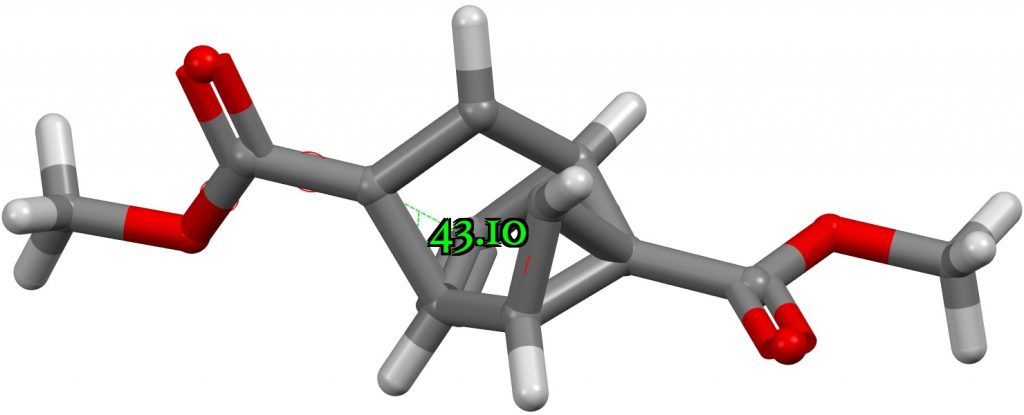
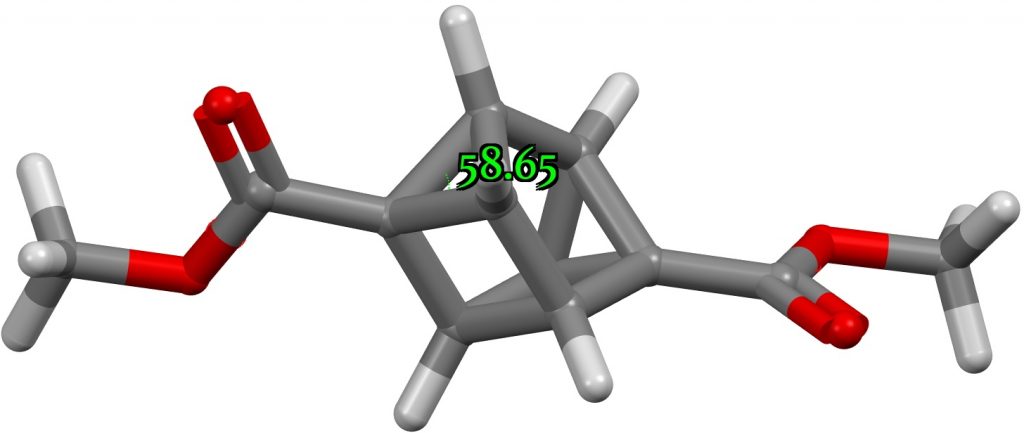
What about the smallest angle at 4-coordinate carbon? Could it be significantly smaller than the 57° noted above for a three membered ring? Searching the CSD reveals XAQHIH[2] with an angle of 43° but the calculation above now does not confirm this, the angle changing from 43° to 59° during optimisation. A reminder that when exploring extreme geometric values, always check with a calculation!
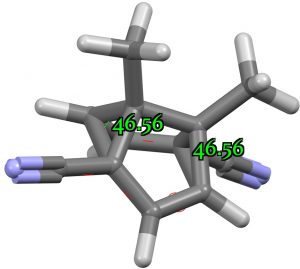
The next candidate is CAZFUE[3] with an apparent measured angle of 48°. This appears to have C2 symmetry, and a calculation with this gives a value of 46.6°. But all is not what it seems. This is a classic example of a semibullvalene [3,3] Cope rearrangement, caught in the “middle” so to speak (See this post here). In fact this geometry is actually a transition state, and the crystal structure is the thermal average of two positions, making it appear symmetrical. The ground state for this structure as calculated is different! The two angles now emerge as 40 and 57° (average 48.6°). At the “transition state”, one of the four “bonds” to carbon is unusually long (2.07Å), which is the direct cause of the small 48° angle. If this is not allowed as a “bond”, the angle at the other true 4-coordinate carbon emerges as normal at 57°
So the answer to the smallest angle does seem to be around 57°, but it could be as small as 47° if one allows bonds of 2.07Å in one’s definition of 4-coordinate. The candidate for the largest bond angle, of almost 180°, seems a reasonable synthetic target!
References
- R. Boese, D. Blaeser, K. Gomann, and U.H. Brinker, "Spiropentane as a tensile spring", Journal of the American Chemical Society, vol. 111, pp. 1501-1503, 1989. https://doi.org/10.1021/ja00186a058
- M.V. Roux, J.Z. Dávalos, P. Jiménez, R. Notario, O. Castaño, J.S. Chickos, W. Hanshaw, H. Zhao, N. Rath, J.F. Liebman, B.S. Farivar, and A. Bashir-Hashemi, "Cubane, Cuneane, and Their Carboxylates: A Calorimetric, Crystallographic, Calculational, and Conceptual Coinvestigation", The Journal of Organic Chemistry, vol. 70, pp. 5461-5470, 2005. https://doi.org/10.1021/jo050471+
- H. Quast, Y. Görlach, J. Christ, E. Peters, K. Peters, H.G. von Schnering, L.M. Jackman, A. Ibar, and A.J. Freyer, "Crystal and molecular structure and the cope activation barriers of some dicyano-1,5-dimethylsemibullvalenes", Tetrahedron Letters, vol. 24, pp. 5595-5598, 1983. https://doi.org/10.1016/s0040-4039(00)94150-9
Tags: Interesting chemistry
Replacing a CH2 with an oxygen in the above opens up the angle even more, to 184°. This now is truly a hemispherical carbon. Removing the group entirely gives an angle of 193.5°.The singlet wavefunction for the latter is stable to open shell states. See DOI: https://doi.org/10.14469/hpc/11148 for more data.