Following from much discussion over the last decade about the nature of C2, a diatomic molecule which some have suggested sustains a quadruple bond between the two carbon atoms, new ideas are now appearing for molecules in which such a bond may also exist between carbon and a transition metal atom. A suggested, albeit hypothetical example was C⩸Fe(CO)3[cite]10.1039/d0cp03436c[/cite]. Iron has a [Ar].3d6.4s2 electronic configuration and if we ionise to balance a C4- ligand, the iron becomes formally FeVI or [Ar].3d4. By adding 14 electrons deriving from the seven “bonds” to the 3d4, including a quadruple count from carbon, the Fe formally completes its 18-electron valence shell, as also found in e.g. Ferrocene.
A search for crystal structures containing the very simple query structure shown below, where C is defined as having one atom only attached, TR is any transition metal and the structure is non-polymeric, was undertaken to see if any examples of this motif might already exist. 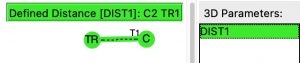
Zero hits with 4-coordinate metal atoms, but 11 real examples were found (FAIR DOI 10.14469/hpc/8190), all of which exhibit a five-coordinate transition metal centre, where X is a mono-anionic ligand (CN, halogen, etc) and L is a neutral ligand (PR3 etc). The most common metal was M = Ru, the electronic configuration of which is [Kr].4d75s1, becoming [Kr].4d2 by ionising to balance a C4- ligand and the two X– ligands. There are now 16 electrons from the eight “bonds” surrounding the atom, including again a quadruple one from the carbon and forming a filled 18-electron valence shell around the metal.
So could these 11 constitute known examples of quadruple bonds from a transition metal to carbon? I will investigate using M=Ru, L = PH3 and X = CN–, which represents a simplified form of one of the 11 examples[cite]10.1021/acs.organomet.5b00803[/cite] using the following electronic model: ωB97XD/Def2-SVPD. The focus will be on five localised NBO orbitals (the procedure I used previously to count the number of bonds at carbon for C⩸Fe(CO)3).
For M=Ru, the NBOs emerge as follows (click on any orbital thumbnail to convert to a 3D rotatable model).
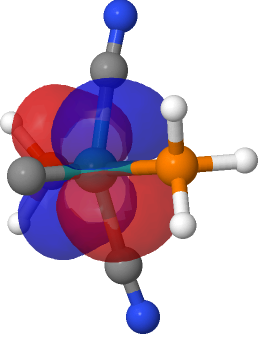
| M=Ru, r = 1.624Å. | |
|---|---|
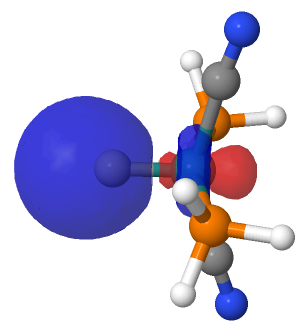
| NBO 42, Occupied, Non-bonding d-orbital | NBO 41 π bond |
 |
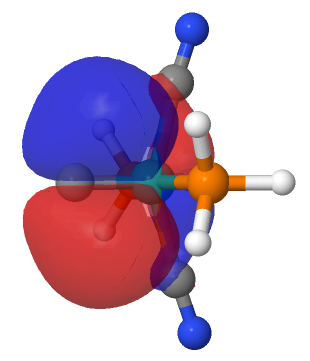 |
| NBO 36 π bond | NBO 35 σ bond |
 |
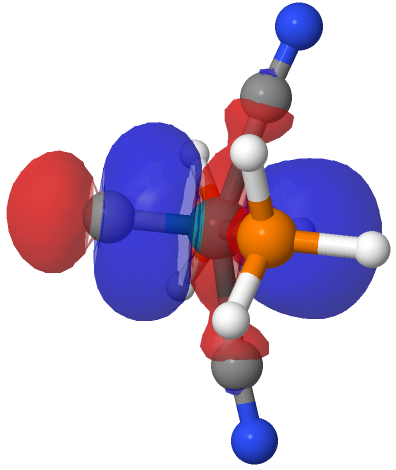 |
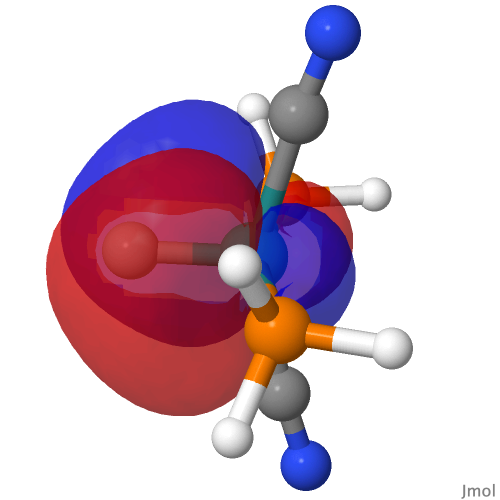
| NBO 34 non-bonding carbon lone pair | Overlap of orbitals 42 and 34 |
 |
|
This reveals only a triple Ru≡C bond plus a non-bonding lone pair on carbon. It turns out that bonding σ-orbital 34 is “surrounded” by the non-bonding Ru d-orbital 42. The electron-electron repulsions between the pair causes the electrons in orbital 34 to locate onto the carbon to form a non-bonding lone pair, as thus:
So might it be possible to persuade this carbon lone pair to instead donate into the M-C bond to form that fully-fledged quadruple bond?
One simple strategy is to remove the two electrons in orbital 42, preventing the Pauli repulsions from occuring and this can be done by using Mo instead of Ru.
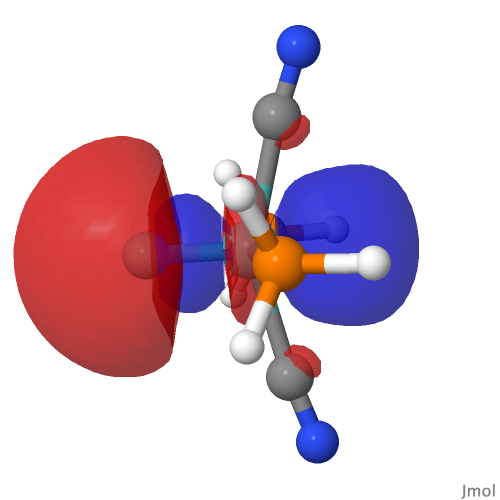
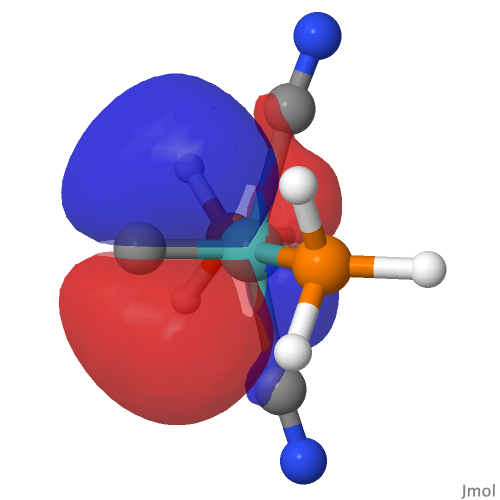
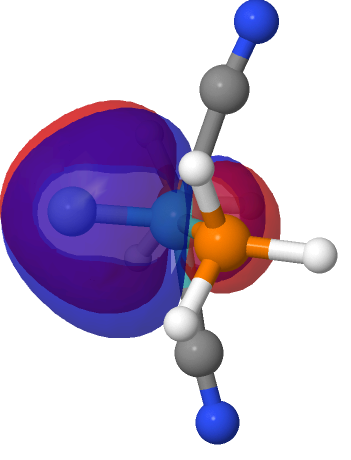
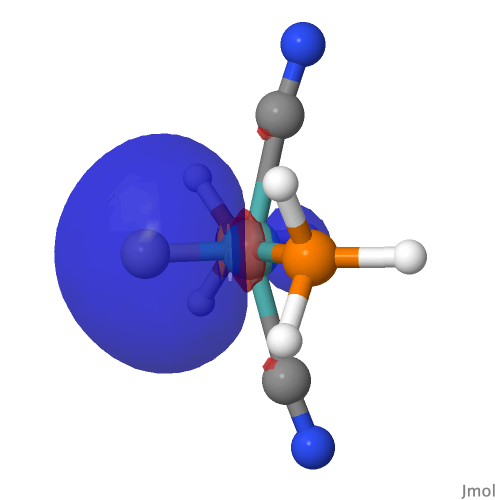
| M=Mo, r = 1.673Å | |||
|---|---|---|---|
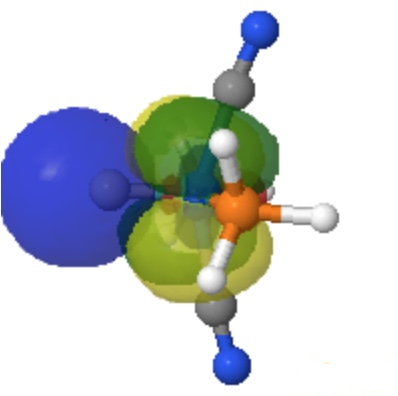
| NBO 42 unoccupied Non-bonding d-orbital | NBO 41 σ bond | ||
 |
 |
||
| NBO 40 π bond | NBO 39 π bond | ||
 |
 |
||
| NBO 22 σ bond | |||
 |
|||
By removing the repulsions to the non-bonding d-orbital, we have now transformed the erstwhile carbon lone pair into a fully fledged bond as in orbital 22, thus forming the quadruple motif. There are two electrons less, so this time the Mo valence shell is a 16-electron system.
So, SUGGESTION 1:
The second possibility is to increase the size of the non-bonding d-orbital 42 by changing from Ru to Os. Here again, orbital 22 is less repelled by the electrons in orbital 42 due to the larger size of the latter and so can again become C-Os bonding rather than non-bonding carbon lone pair.
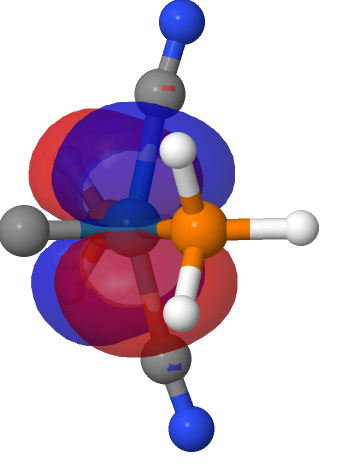
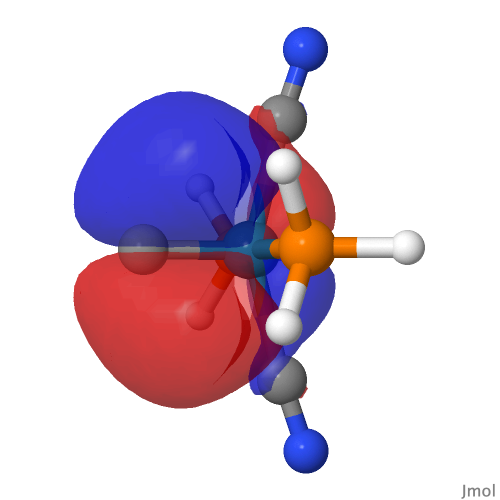
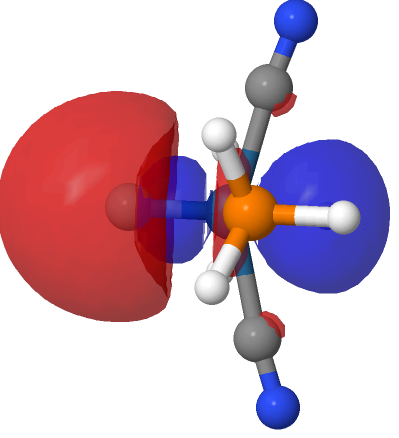
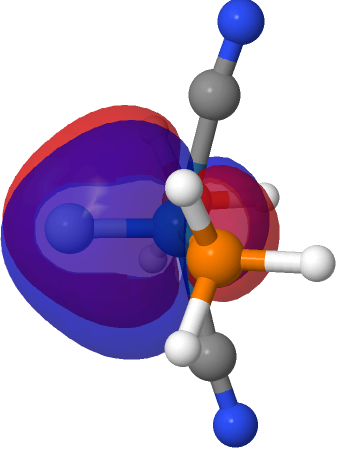
| M=Os, r = 1.679Å | |||
|---|---|---|---|
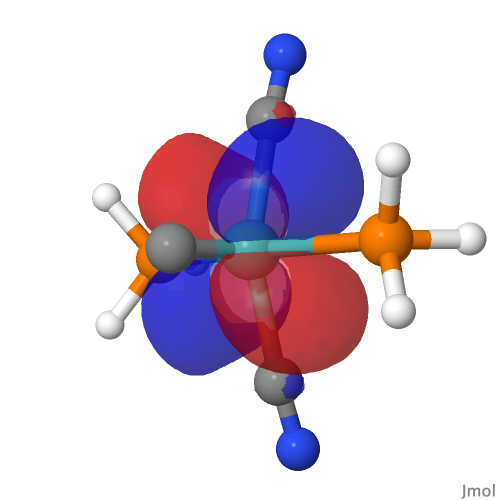
| NBO 42 Occupied Non-bonding d-orbital | NBO 41 π bond | ||
 |
 |
||
| NBO 40 σ bond | NBO 35 π bond | ||
 |
 |
||
| NBO 22 σ bond | |||
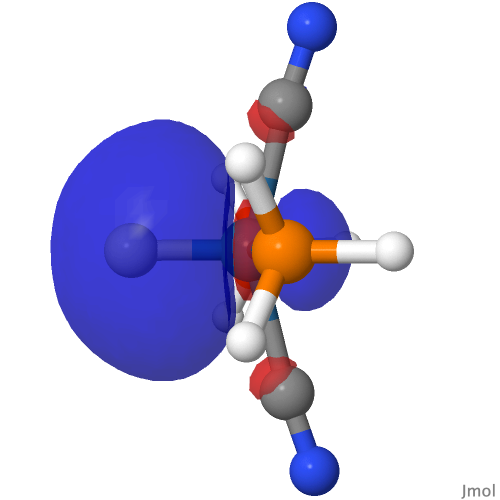 |
|||
So, SUGGESTION 2
This approach also reveals the binary decision in the NBO analysis, either an orbital is classified as “LP” and hence is not considered a bond, or it is classified as “BD” and is a bond. Reality is certainly more nuanced, with weights needing to be assigned to each valence bond representation (rather than just 1.0 or 0.0). Probably also these weights will depend on a number of factors, such as basis set quality and the method applied (e.g. the DFT procedure used). So the binary terms “triple” or “quadruple” do not carry the full measure of the bonding behaviour, which may be a continuum between these two extremes. But the two molecules shown above do represent molecules that could be realistically synthesized, since they are but small variations of already known molecules. Once made, they could then be subjected to appropriate experimental analysis to test the bonding hypotheses made here.
This post has DOI: https://doi.org/gbq3