This is one of those posts of a molecule whose very structure is interesting enough to merit a picture and a 3D model. The study[cite]10.1126/science.aal1619[/cite] reports a molecular knot with the remarkable number of eight crossings.
The DOI for the 3D model is 10.5517/CCDC.CSD.CC1M85Y0 (or click on the image above). Such topology intersects with work we did a few years back on high-order crossings in fully conjugated π-systems[cite]10.1021/ja710438j[/cite], which were then illustrated[cite]10.1021/jp902176a[/cite] with hypothetical charged higher order annulenes exhibiting linking numbers Lk of up to 6π. A fully π-conjugated system, also with a linking number in the π-framework of 6π but in the form of a trefoil braid was even suggested on this blog, with a common feature of a central templating atom (a cation rather than an anion). Another example of a previously reported pentadecanuclear manganese metallacycle[cite]10.1021/ic800987f[/cite] was also assigned a linking number of 6π.
The molecule above is not completely π-conjugated around the braid and so special properties related to aromaticity and associated ring currents resulting from the topology of the cyclic conjugation[cite]10.1016/j.comptc.2014.09.028[/cite] are not expected to accrue in the eight-crossing molecular braid[cite]10.1126/science.aal1619[/cite]. We might also look forward to examples of the characterisation of braids with an odd-number of crossings such as trefoils, pentafoils, heptafoils, etc, as associated with the name Möbius.
Tags: Cheminformatics, Chemistry, Drug discovery, Education, π-systems, Matter, Molecule, Nature, spectroscopy, Structure validation
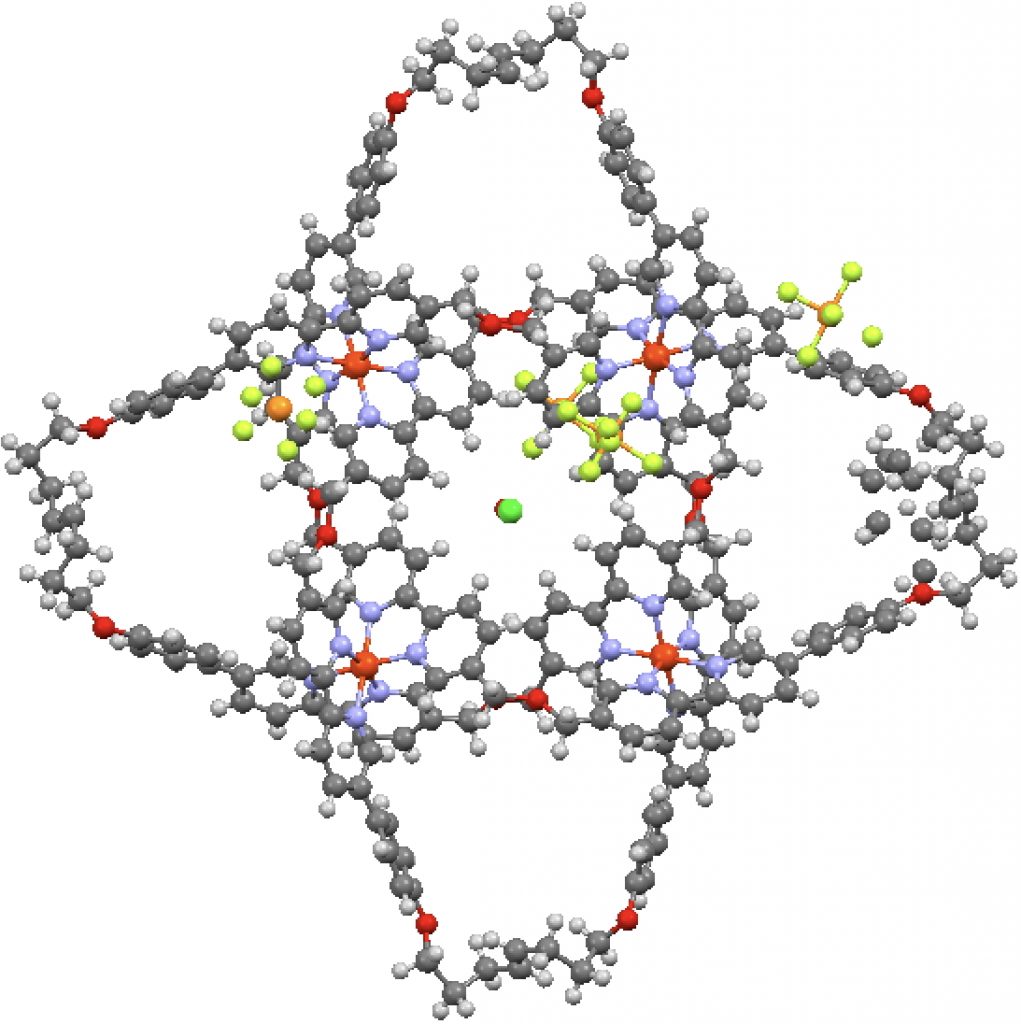
A hexafoil knot (Star of David) is reported by the Leigh group, DOI: 10.1038/nchem.2056, 3D Model DOI: 10.5517/CC129N45.
A pentafoil knot is also reported, DOI: 10.1126/science.aaf3673, 3D Model DOI: 10.5517/CCDC.CSD.CC1KFN3R.
In another post, I noted Derek Lowe’s book on 250 milestones in chemistry, highlighting two entries. As the same time, I also got Clifford Pickover’s book on 250 milestones in mathematics. You might expect that knots feature in this book. Again, I note two interesting entries.
1. Pickover places the discovery of knots at around 100,000 BC. He also mentions (and he was writing in 2009) that around 1.7 million non-equivalent knots with 16 or fewer crossings have been discovered.
2. His second milestone dates from 1988 when Sumners and Whittington (the latter a chemist) modelled ropes and other objects such as polymer chains, finding using purely mathematical procedures that nearly all sufficiently long self avoiding random walks will contain a knot (DOI: 10.1088/0305-4470/21/7/030), or more specifically that for n steps in a random walk, the knot probability goes to unity as n goes to ∞.
3. Finally, I note that Wikipedia has a whole section on knotted proteins, including trefoils. The topic of knotted proteins is a recent one, the first suggestions being in 1994!
A search of the protein databank (PDB) as http://www.rcsb.org/pdb/search/advSearch.do?search=new reveals 39 systems described by the term trefoil!