In the previous post, I suggested that inspecting the imaginary modes of planar cyclohexane might be a fruitful and systematic way in which at least parts of the conformational surface of this ring might be probed. Here, the same process is conducted for cyclo-octane. The ring starts with planar D8h symmetry, and at this geometry (B3LYP/6-311G(d,p), DOI: 10042/to-3742) five negative force constants (corresponding to imaginary modes) are calculated. The most negative is non-degenerate, and gives directly the crown conformation of D4d symmetry (DOI: 10042/to-3738). The remaining four modes comprise two degenerate pairs. Following either of the E2u eigenvectors downhill leads to another conformation, D2d (DOI: 10042/to-3741), with a geometry which is noteworthy for exhibiting a pair of unusually close non-bonded H…H contacts (1.908Å). This value is about 0.3Å shorter than the sum of the Wan der Waals radii (DOI: 10.1021/jp8111556). We can debate whether such a close approach or inter-penetration of two hydrogens is a bond or not (an AIM analysis appears at the bottom of this post).
| D8h, +82.8 kcal/mol | ||
|---|---|---|
| Follow B2u 467i | Follow E3g 404i | Follow E2u 230i |
| to D4d +0.8 | to Ci 131i (Au), +7.5 | to D2d +3.6 |
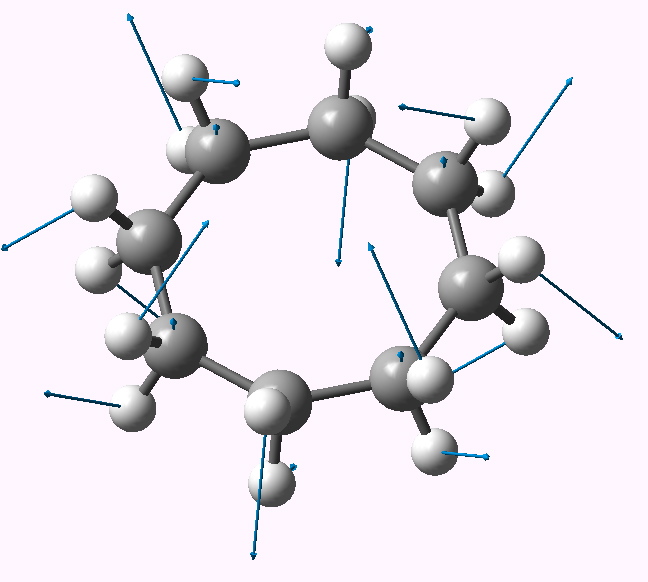 B2u |
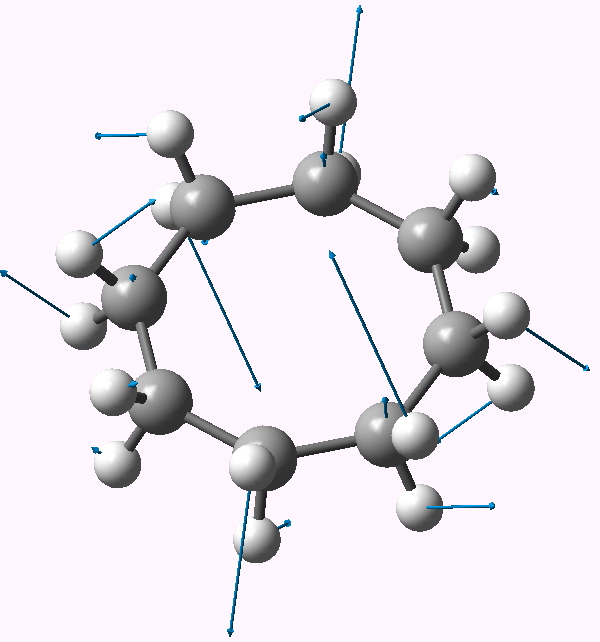 E3g |
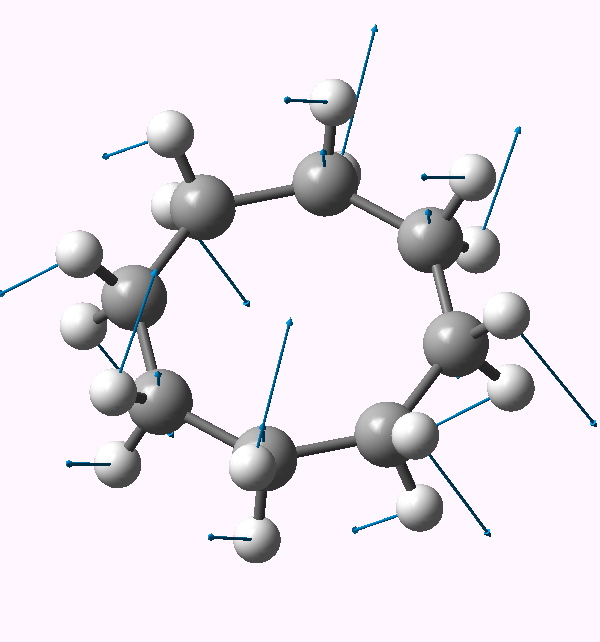 E2u |
| Cs 0.0 | C2 +1.6 | – |
Following the remaining E3g mode leads to a stationary point of Ci symmetry (DOI: 10042/to-3743). This is a valley-ridge potential, since this point turns out to be a transition state itself, and following the Au imaginary mode at this point results in another, this time stable conformation, of chiral C2 symmetry (DOI: 10042/to-3744). This has a calculated optical rotation [α]D of 72° (at 589nm in chloroform).
Are these three conformations all there are? Well, a thorough analysis of the conformational space has in fact identified six minima (DOI: 10.1002/(SICI)1096-987X(19980415)19:5<524::AID-JCC5>3.0.CO;2-O), of which the most stable has Cs symmetry (the so-called chair-boat conformation, and the one most frequently found in crystal structures of cyclo-octanes). Where is that one in the above analysis? It arrives by a distortion of the D4d form (DOI: 10042/to-3747) via a transition state of no symmetry (DOI: 10042/to-3752)
Whilst the full potential surface clearly has many more features, following the modes of the planar conformation of cyclo-octane is a simple and rapid way of establishing four of the six limiting stable conformations (the two remaining forms have D2 and S4 symmetry, see DOI 10.1016/0166-1280(88)80008-3).
Finally as promised, the AIM analysis of the D2d conformer (above). The ρ(r) value at the interesting H…H critical point is 0.015, which is pretty high in comparison to most normal hydrogen bonds, and would be conventionally taken to indicate attraction. The Laplacian ∇2ρ(r) is +0.05. The “bond” ellipticity ε has a value of 0.29. Single bonds are close to zero, and C=C double bonds are ~0.4, so this is pretty high (see also DOI: 10.1002/anie.200805751).
The two highest C-H stretching vibrations for this conformation are well separated from all the others (ν 3095, 3103 cm-1 for the symmetric A1 and antisymmetric B2 combinations, below for animations). These vibrations serve to both decrease and increase the H…H distances as part of the atomic (harmonic) displacements, and clearly doing so takes more energy than vibrating any of the other C-H bonds. It seems unlikely that the C-H bonds are themselves stronger, so does that mean that the H…H interaction is attractive or is it repulsive? In this context, it is worth noting that the symmetric vibration (both H…H distances decrease/increase at the same time) is lower in wavenumber than the mode which decreases one and increases the other.
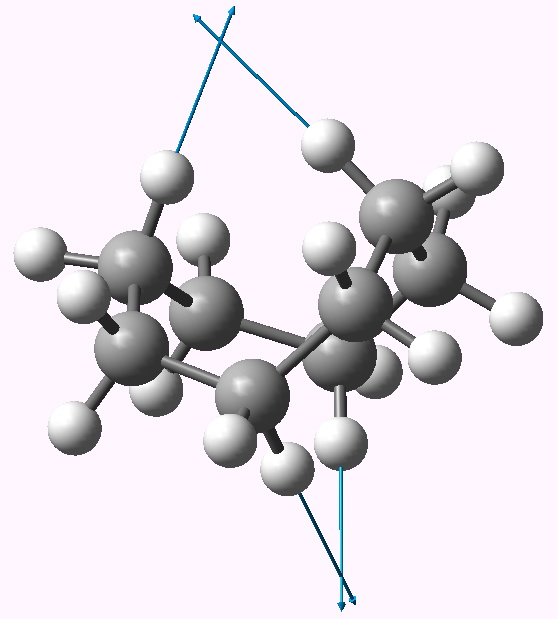 A1 |
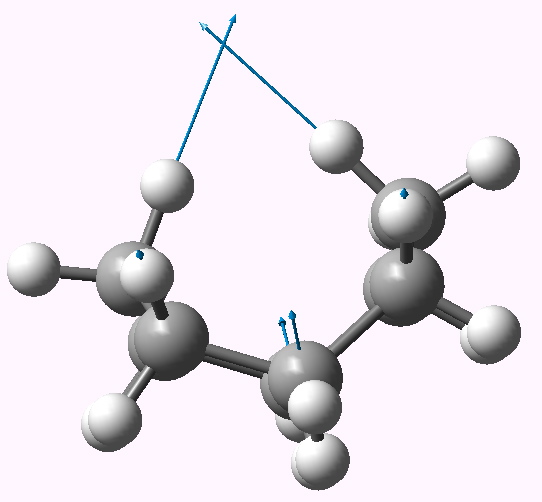 B2 |
Tags: 3g, conformational analysis, cuyclooctane, energy, General

An addendum to the comment in the post relating to whether the H…H interaction in the D2d symmetric conformation might be attractive or repulsive. I decided to see if the calculated anharmonic frequencies might cast light on this issue. The argument was as follows. The A1 vibrational mode decreases both H…H distances simultaneously. If the H…H interaction was attractive, then the potential might be distorted and the mode would be expected to become more anharmonic. The B2 vibration, for which one H…H distance increases and the other decreases, might self-compensate and the anharmonic correction would be smaller. If the H…H region is in fact repulsive, the reverse would be true, ie the A1 mode would exhibit a smaller anharmonic effect than the B2.
The results are as follows. The harmonic frequencies for the A1 and B2 are respectively 3096 and 3103 cm-1; the anharmonic values (DOI: 10042/to-3768) are 3001 and 2983 (note that the anharmonic correction makes the frequencies much more compatible with experiment). This does seem to come down in favour of the H…H region being repulsive!
Issue settled then! (?)