Henry Rzepa's Blog

The electrophilic substitution of indoles is a staple of any course on organic chemistry. Indoles also hold a soft-spot for me, since I synthesized not a few as part of my Ph.D. studies.[cite]10.1039/P29750001209[/cite],[cite]10.1039/P29770000281[/cite] The preference for substitution in the 3-position is normally explained using the arrows shown below (position 3=green,2=blue,1=red). Here I explore how these arrows might be interpreted in terms of various quantum mechanical properties.

I have elsewhere in these posts shown how NBO (natural bond orbitals) can often be used to probe donor-acceptor interactions in molecules. Can it be applied to indole (as donor) interacting with an electrophile (as acceptor) in order to predict where the most nucleophilic centre is? The law is that the pair of such filled/empty orbitals with the lowest energy gap will predict the reactivity. Since the electrophile E is common, we might presume that the NBO donor orbital with the highest energy is the relevant predictor. Well, this emerges as the NBO describing the 8,9 bond; it is not any of those shown above! The next NBO in energy is also located on the benzo group. Only the 3rd-highest NBO corresponds to the red arrows above. In fact the NBO with the least-favourable energy is the one that maps to positions 2 or 3, those normally implicated in the reactions of this molecule. What has gone wrong?

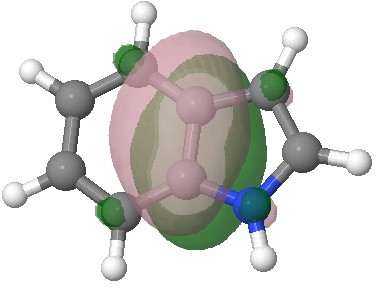E=-0.2910au. 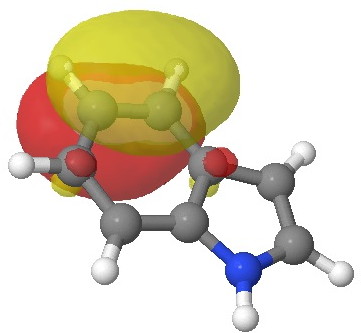Click for 3D	E=-0.3107au. Click for 3D
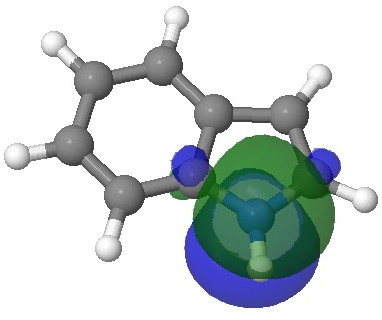E=-0.3113au. 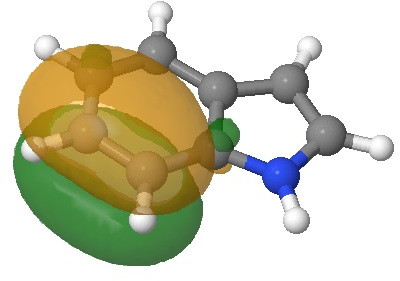Click for 3D	E=-0.3142au. 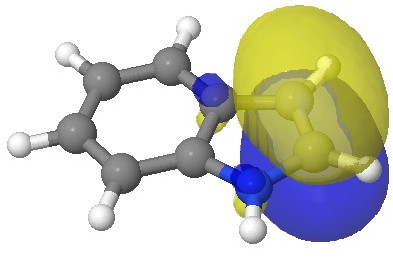Click for 3D	E=-0.3335au. Click for 3D

To start understanding, we must review the assumptions made in the above analysis.

1. Firstly, we need to distinguish between local and global properties of molecules. A local property is one e.g. associated perhaps with an atom or bond. A global property might be the aromaticity of the system as a whole. The NBO analysis, by definition, tries to localise the wavefunction to one or two centres. This means that it reduces a six-electron aromatic ring to three two-centre bonds. But breaking up an aromatic ring may not be the best way of looking at the problem. In this case, the 2,3 N=C bond emerges as the most stable double bond, largely because the six electrons of the benzo group are delocalised and hence not so stable locally! So too much localisation can throw the baby away with the bath water. So let us try a rather more global property, the molecular electrostatic potential (MEP):
   
   

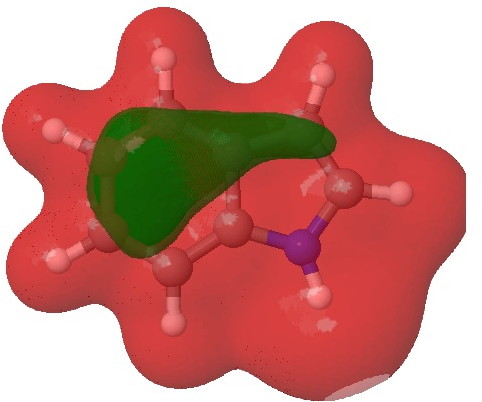
   Molecular electrostatic potential. Click for 3D.

   This probes the molecule for regions which are the most attractive to a proton (=E⁺). Perhaps surprisingly, the benzo group still emerges as the most attractive region, but at least there is a small attractive finger (green) that reaches out to the 3-position rather than the 2-position (the “right” answer). It is not entirely convincing though, is it?

2. Which leads us on to another assumption, which invokes Hammond’s postulate that the transition state for the reaction will resemble the stable species nearest to it in free energy. What if the transition state (which is what determines the rate of a reaction) more closely resembles the (initial) product of this reaction, the so-called Wheland intermediate rather than indole itself? I am going to calculate this intermediate in a novel manner; as an ion-pair resulting from reaction of indole with HCl in methanol (I have blogged elsewhere that I regard it as lazy to simple add a proton and put +1 as the overall charge of the system). So here are the relative free energies of indole reacted with HCl in respectively the 1,2 and 3 positions: 4.1, 10.0, 0.0 kcal/mol.The relatively high energy of the 2-substituted intermediate reflects its loss of global aromaticity compared to the other two, rather than necessarily any local property. 
   
   

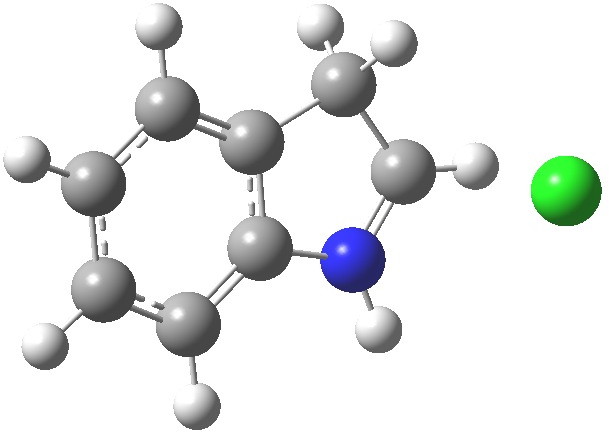
   3-Wheland intermediate. Click for 3D.

   We might therefore conclude that one should not seek evidence in the wavefunction of indole itself for the preference for green rather than blue or red arrows as shown above, but in a reaction product which best reflects the global properties such as aromaticity.

3. One could go one stage further and actually locate explicit transition states for the three isomeric reactions, as was done here. I may report back on this in the future.

I set out these approaches aware that a subject is often taught by reducing it to rules (heuristics) which one then hopes are transferable between different molecules with common local or global features. One does not want to reduce it down merely to numbers computed from a wave equation. But one should also remember that whilst arrow-pushing may be fine for relatively simple systems, it may not be robust towards increasing complexity (i.e. multiple substituents around the ring). At some stage, one will have to take the decision to augment the simple heuristics with computed numbers. Deciding when to do so will be one of the challenges facing the teaching of chemistry over the next decade.

Tags: benzo, energy, least-favourable energy, lowest energy gap, Reaction Mechanism, reaction product, Tutorial material

This entry was posted on Sunday, March 3rd, 2013 at 11:49 am and is filed under Interesting chemistry. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.