We tend to think of simple hydrocarbons as relatively inert and un-interesting molecules. However, a recent article[cite]10.1002/anie.201202894[/cite], which was in fact highlighted by Steve Bachrach on his blog , asks what “The Last Globally Stable Extended Alkane” might be. In other words, at what stage does a straight-chain hydrocarbon fold back upon itself, and no significant population of the linear form remain? The answer was suggested to be C17H36. I thought I might subject this conformation to an NCI (non-covalent-interaction) analysis.
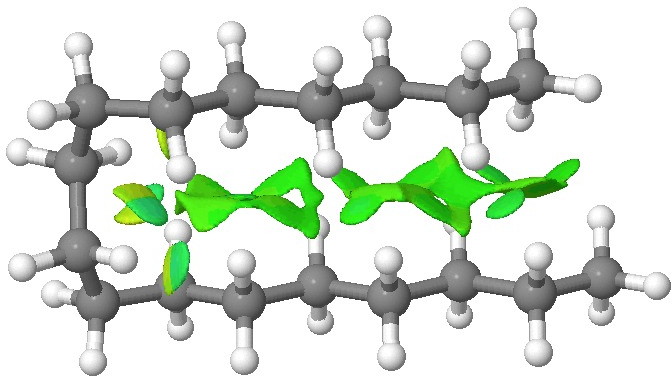
NCI analysis. Click for 3D.
The colour coding for the NCI surface is such that towards blue is attractive, with green being mildly attractive and yellow mildly repulsive. Both blue and yellow can be seen at the point where the molecule bends round, and attractive green dominates the region where the two chains are parallel. Much in the manner of a Gekko’s feet[cite]10.1002/adfm.201100493[/cite], the strangely attractive van der Waals terms in a hydrocarbon are surprisingly cumulative! You can generate an NCI surface for your favourite molecule here.
Addendum: To show that NCI interactions are pretty additive, here is C28H58:
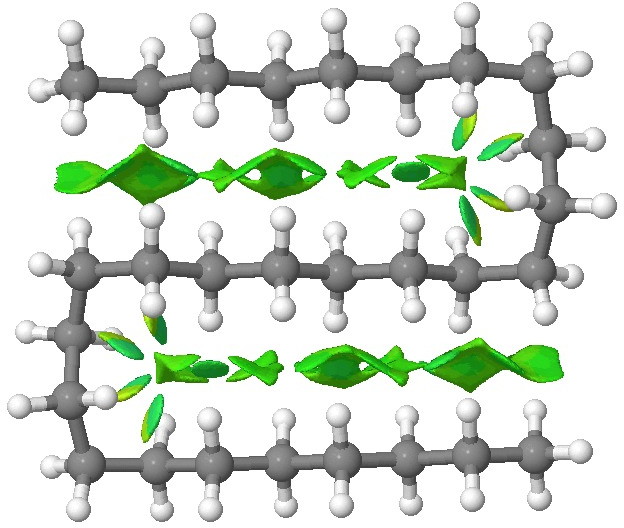
C28 double hairpin. Click for 3D.
Tags: conformational analysis, Steve Bachrach, Tutorial material
Instructive illustration, Henry, but butane is the “last globally extended n-alkane” in the gas phase at 25 deg C (the “standard” conditions). Entropy favors gauche (over extended) conformations due to their lower symmetries and chirality. Thus, the C1 gauche conformation of n-pentane has a lower free energy that its zig-zag (C2v) conformation.
Thanks Paul. I understand how lower symmetry might impact upon the free energy (it presumably comes in from the symmetry number correction to the entropy). But how might chirality play a role in the free energy (unless it is via that same symmetry number)?
There is some very old electron diffraction work by Bartell and Kohl on heptane which suggests that the amount of the all anti conformation is about 16% (DOI: 10.1063/1.1734149). Has that result perhaps been shown to be incorrect or inaccurate?
Dear Henry
The entropy gain upon racemization of two entantiomers is R ln 2. Individual enantiomers must have higher FREE energies than their racemates (or else why would racemization take place?).
The symmetry number of the singe gauche n-pentane conformation is one vs. two for the zig-zag (C2v) conformation. This adds another R ln 2 to the entropy difference. Statistically, four identical gauche C1 conformations are possible vs. only one C2v conformation
At RT, n-butane is 36% gauche and 64% anti, whereas n=pentane is 51% mono gauche, about 10% double gauche (C2), and the rest C2v (from memory). The larger the alkane, the smaller the amount of the all-anti conformation.
The point about recemisation reducing free energy by R ln 2 is obvious, but not something I had previously picked up on. I have learnt something!
So pentane still has about 40% all anti, heptane it appears to reduce to about 16%, and we may presume that it drops to effectively zero at some stage above heptane (but probably well before C17 is reached). As you point out, the density of states for the all anti is low, whereas the number of equivalent configurations for the gauche forms is far higher, which alone starts to favour them.