I return to this reaction one more time. Trying to explain why it is enantioselective for the epoxide product poses peculiar difficulties. Most of the substituents can adopt one of several conformations, and some exploration of this conformational space is needed.
Amongst the conformational possibilities are the two rotations shown below. The blue rotates the ester with respect to the Ti-O-C unit, and the red rotates within the ester group itself. In fact the conformations of esters almost invariably adopt the first conformation shown, a s-cis orientation where one lone pair from the alkoxy group is anti to the axis of the carbonyl group (red rotation). Crystal structures of binuclear titanoxy compounds show both options for the blue rotation.
One might imagine that there are two rotations about the C-O and O-Ti bonds in the iPr-O-Ti fragment as well. Whilst some of the many permutations are precluded simply on steric grounds, this still leaves a lot of possibilities. I have certainly not explored anything like the full set, but felt it worth reporting two conformations which have lower energies than the ones I reported in this post. If I find any yet lower in energy, I will add a postscript here.
| New conformations (hydrogens removed for clarity) | |
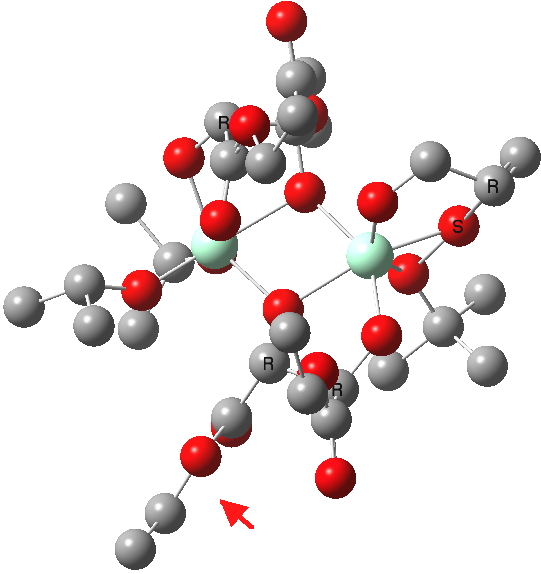 (R). Click for 3D |
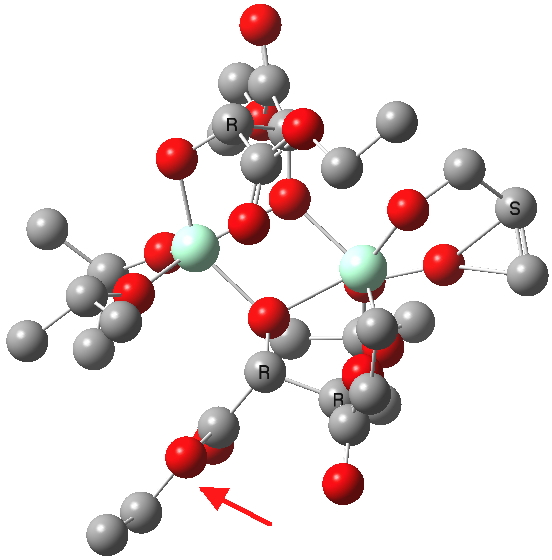 (S). Click for 3D. |
| Old conformations | |
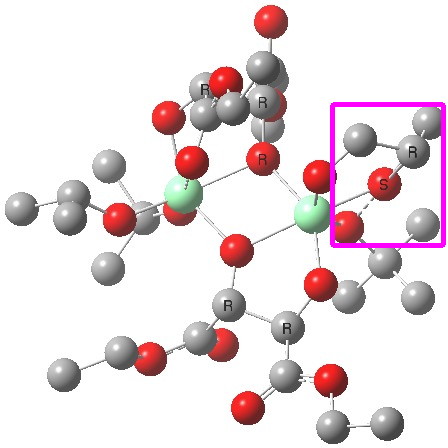 (R). Click for 3D. |
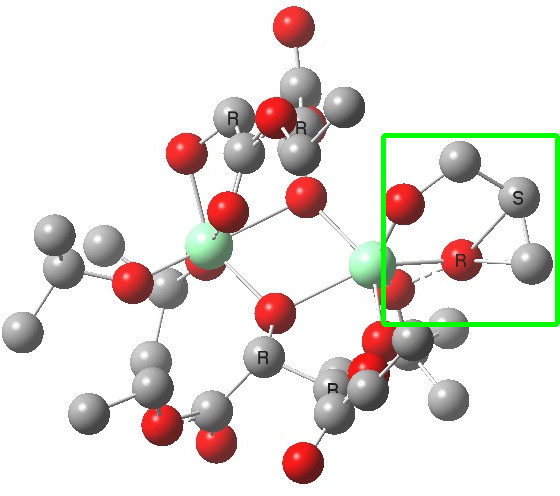 (S). Click for 3D |
The conformations differ in the regions indicated with a red arrow; the (R) being 10.1 and the (S) 7.5 kcal/mol lower in ΔG298. Note how a change in conformation of just one group can “knock-on” to other groups. The relative energies (kcal/mol) of these two new conformations are shown below, broken down into three components.
| Enantiomer | Total energy | Attractive dispersion energy | Free energy |
| R | +2.2 | +2.9 | +0.3 |
| S | 0.0 | 0.0 | 0.0 |
As before, (S) wins out clearly in terms of the dispersion attractions, which appears to be also reflected in the total energy of each system (in other words, differentiation from non-dispersion terms is not large). The free energy includes the entropy calculated from the normal vibrational modes using the rigid-rotor-harmonic-oscillator approximation. Whilst it too shows (S) to be the lower in energy, the distinction is less clear-cut than with the old conformations. One is often warned that the RRHO oscillator approximation is not good for molecules with many free rotors (which normally means about single bonds), although one normally might expect that comparing two very similar systems will result in a lot of cancellation of errors. But this result here does suggest that for the Sharpless system, which has many free-rotor groups, free energies might need taking with an extra dose of caution. I would also add that one does need to optimise the geometry of transition states for such systems with extraordinary accuracy; for these two examples, one does need to achieve values for the six “zero” translations and rotations of < 10 cm-1, which can involve heroic efforts (as it did here!).
I end by reiterating my earlier conclusion. The Sharpless seems to be an example of a reaction which achieves stereospecificity by the accumulation of many very tiny effects (the dispersion attractions), and hence the use of a dispersion-corrected method is absolutely critical. It may also in part involve accumulation of another set of small effects contributing to the total entropy and hence free energy. What it appears not to be is a manifestation of a small number of larger effects (e.g. stereoelectronic alignments) which can be “named”. Chemistry by and large is always an attempt to achieve simple explanations by use of the latter; in other words developing simple heuristics or rules that can be transferred between systems. Where you have an effect that is in effect an accumulation of many terms, it is much more difficult to express this as simple transferable rules. Chemistry at such a level then is reduced simply to computing the sum of these small effects, rather than relying on simple rules. Have we perhaps reached this level with the Sharpless per-epoxidation? Would it be such fun if it were?
Tags: catalysis, conformational analysis, energy, epoxide product, free energy, Reaction Mechanism, similar systems, Tutorial material