Most scientific theories emerge slowly, over decades, but others emerge fully formed virtually overnight as it were (think Einstein in 1905). A third category is the supernova type, burning brightly for a short while, but then vanishing (almost) without trace shortly thereafter. The structure of DNA (of which I have blogged elsewhere) belongs to the second class, whilst one of the brightest (and now entirely forgotten) examples of the supernova type concerns the structure of proteins. In 1936, it must have seemed a sure bet that the first person to come up with a successful theory of the origins of the (non-random) relatively rigid structure of proteins would inevitably win a Nobel prize. Of course this did happen for that other biologically important system, DNA, some 17 years later. Compelling structures for larger molecules providing reliable atom-atom distances based on crystallography were still in the future in 1936, and so structural theories contained a fair element of speculation and hopefully inspired guesswork (much as cosmological theories appear to have nowadays!).
Dorothy Wrinch was a mathematician who came up with just such a hypothesis for rigid protein structure, based in effect on elegance and symmetry, coupled with some knowledge of chemistry and crystallography[cite]10.1098/rspa.1937.0159[/cite]. She had noticed that the repeating polypeptide motif might be folded such that a cyclisation could occur to give what she termed a cyclol (an organic chemist would call this an aminol, and we would also now recognize it as a three-fold tetrahedral intermediate of the type involved in the hydrolysis of peptides). Wrinch proposed that this cyclisation could be repeated on a large scale to produce rigid scaffolds for proteins. The three-fold symmetric elegance of such motifs clearly appealed to this mathematician (the interesting symmetrical and conformational properties of the central cyclohexane-like ring were still to be fully recognised by anyone. Since Wrinch built many 3D models of her cyclols, one can but wonder how that central ring was represented, and whether its chair conformation was at all recognised. Another Nobel prize awaited the discoverer of this, Derek Barton).
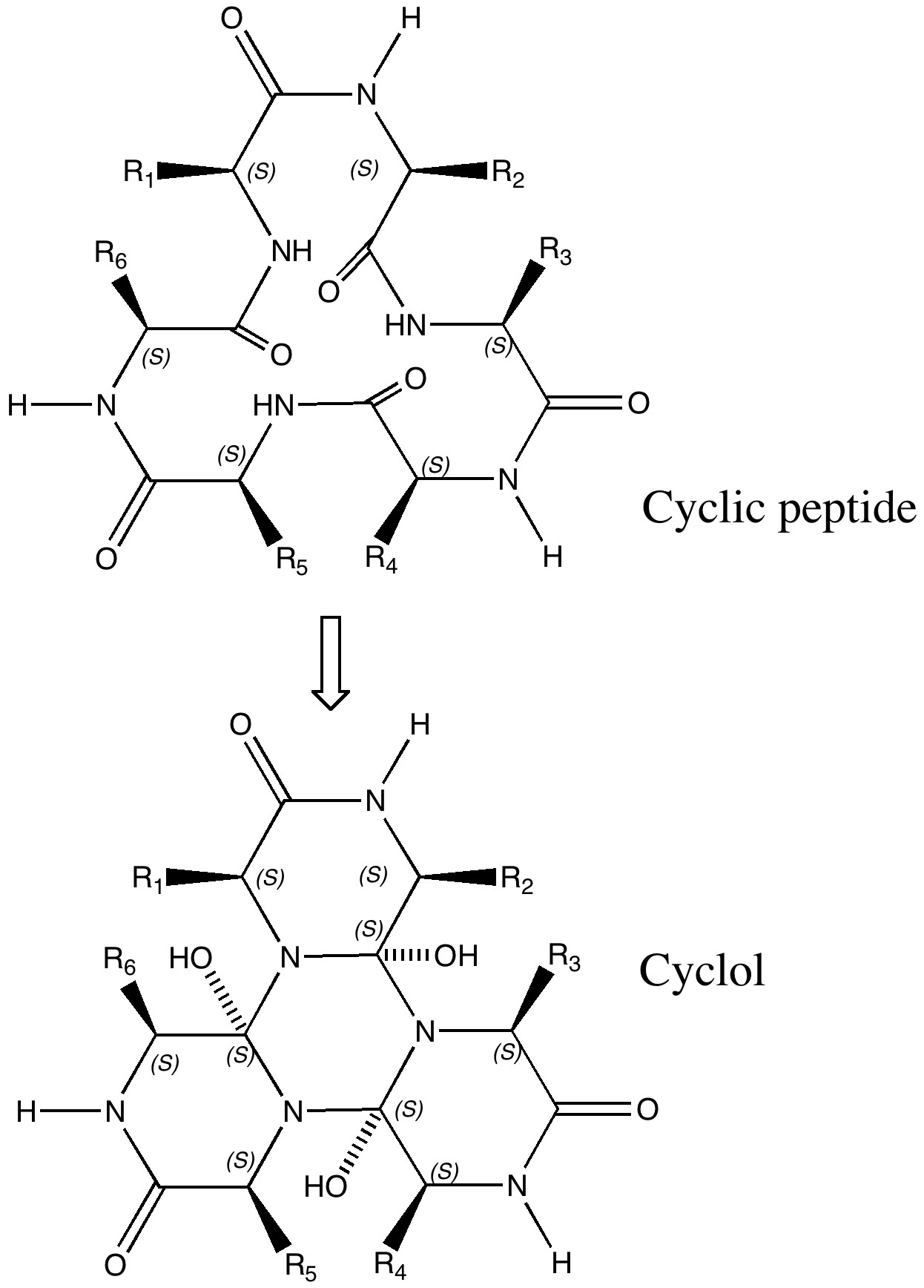
The Cyclol structure. Click for 3D.
An immense controversy immediately broke out (not least because little direct spectroscopic evidence for the OH groups could be found). The story is rivetingly told by Patrick Coffey in his book Cathedrals of Science (ISBN 978-0-19-532134-0). Linus Pauling entered the fray in 1939[cite]10.1021/ja01876a065[/cite], and one of the arguments he deployed was not so much symmetric elegance but thermodynamics (he also suggested hydrogen bonding and S-S linkages for rigidifying proteins). The proposed cyclisation, he suggested, led to a very high energy species. Whilst Wrinch attempted to refute this[cite]10.1021/ja01847a004[/cite], Pauling’s arguments won almost everyone over. Although Wrinch forlornly continued to promote her idea, last reviewing the topic as late as in 1963[cite]10.1038/199564a0[/cite], crystallography was now producing cast iron data for protein structures. None have ever emerged with a cyclol motif, and this hypothesis is now firmly consigned to untaught history[cite]10.1002/pro.5560060627[/cite]. To this day, no examples of the tris(aminol) cyclol ring are to be found in the Cambridge small molecule crystal structure database either, although some related tetrahedral intermediates are known as crystalline species (see for example here) and they can be quite easily characterised in solution.[cite]10.1021/ed064p725[/cite]
When I read the story, it struck me that modern theory could easily verify how valid Pauling's thermodynamic argument was. I have picked (ala)6 as my model, and have calculated the relative free energy (ΔG298) of the following three isomers.
-
An acyclic zwitterionic form of this hexapeptide, calculated with a SCRF reaction field for water to allow for the ionic nature (ωB97XD/6-31G(d,p)), reveals a proton transfer to a neutral system, with an energy of +7.3 kcal/mol
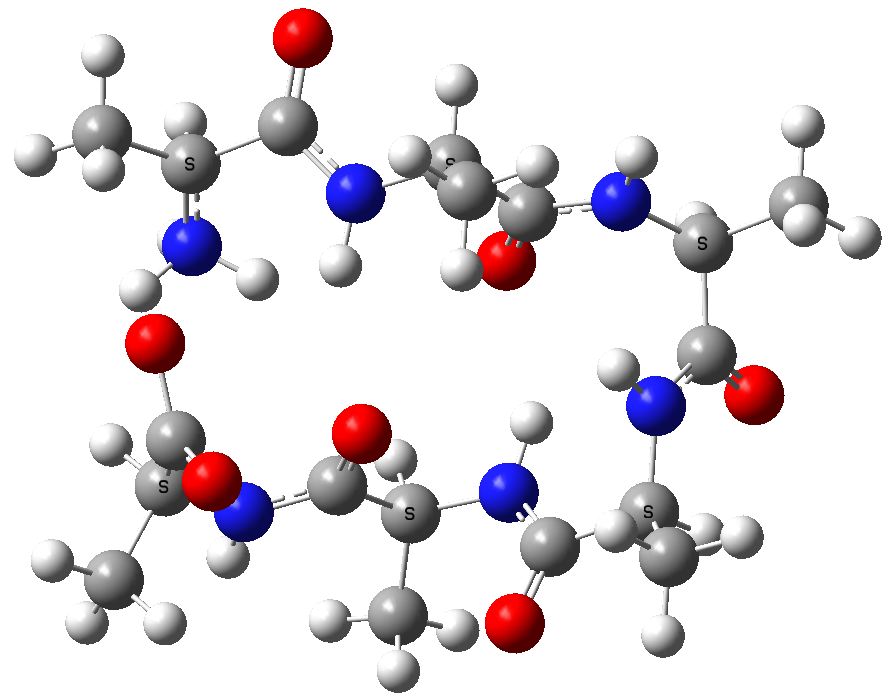
Acyclic (ala)6, in zwitterionic form
-
A cyclic neutral peptide, which results from elimination of water from 1, again calculated with a water reaction field[cite]10.14469/ch/8194[/cite], revealing a relative free energy of +0.0 kcal/mol
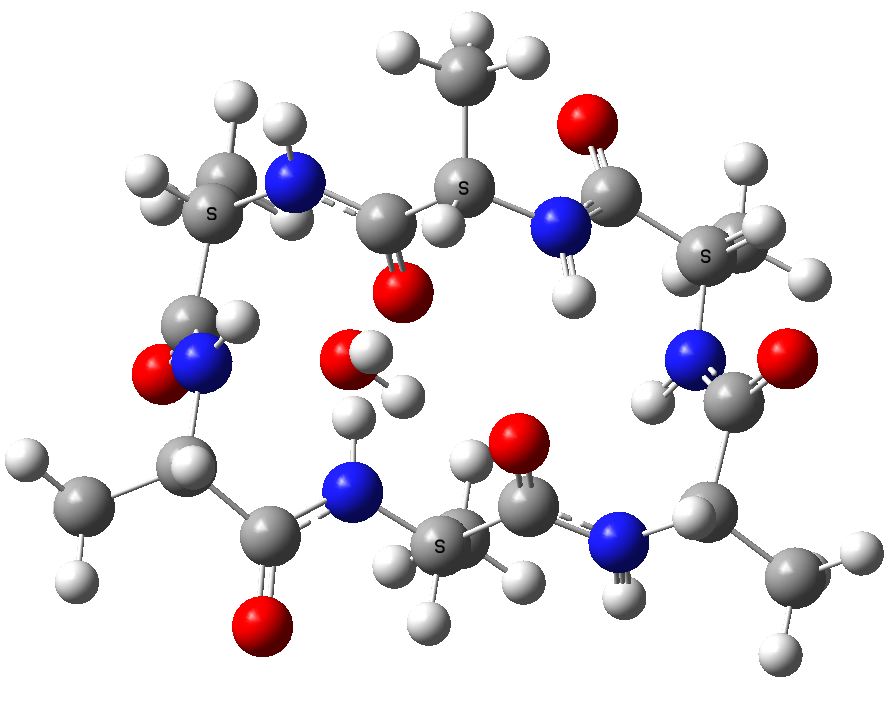
Cyclic (ala)6
-
The cyclic isomer 3 resulting from further cyclisation of 2[cite]10.14469/ch/8197[/cite] with a relative free energy of +69.0 kcal/mol
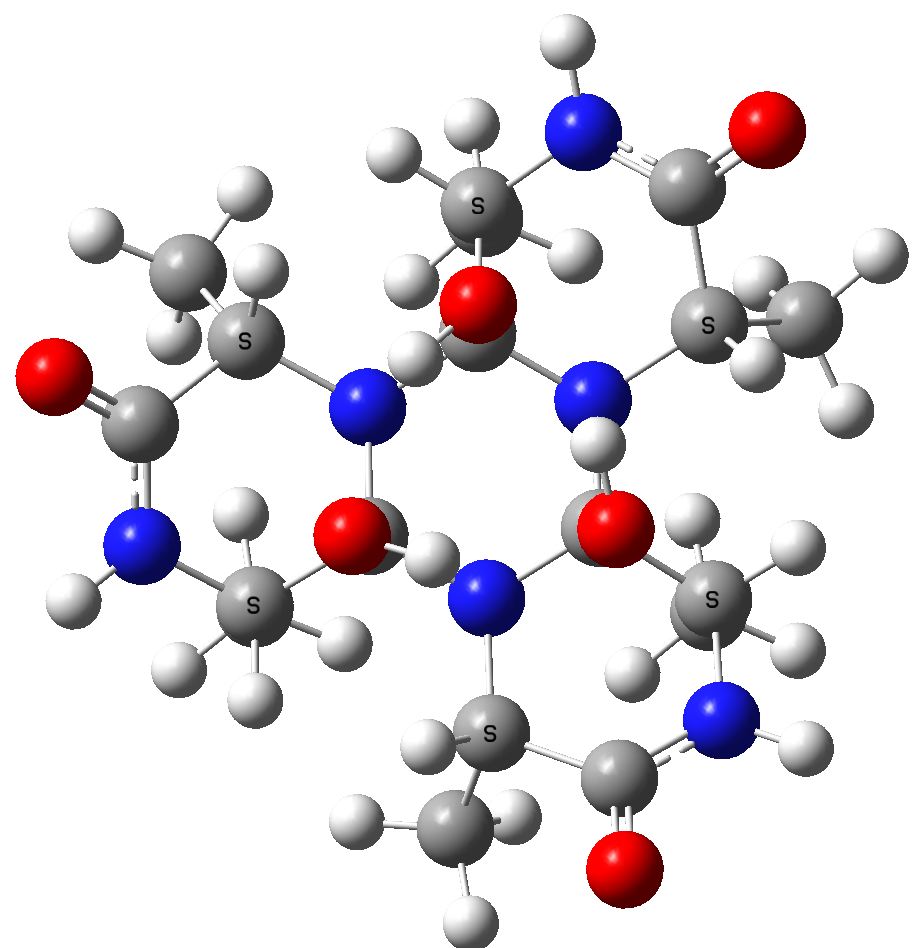
Cyclol model for (ala)6.
From this, it appears that model 3 is ~69 kcal/mol less stable than the cyclic peptide 2, or 11.6 kcal/mol per amino acid residue. Pauling's thermodynamic arguments suggested a value of ~28 kcal/mol per residue (a value which Wrinch disputed as unreliable). So, in one sense, the above calculation is closer to Wrinch than to Pauling! In another, it still means Wrinch was wrong!! It is worth speculating why Pauling's estimate is out. The cyclol 3 exhibits anomeric stabilizations, which of course were unknown in Pauling's time. Both 2 and 3 exhibit attractive, but different, van der Waals attractions which contribute to their stabilities and Pauling took no account of any entropy differences between 2 and 3. In retrospect, 3 was simply too rigid to allow most enzyme catalysis models to function, as we recognise them nowadays.
You might ask why I have revived a long forgotten theory as the topic of this post. Well, I think it is always worth revisiting the past, and re-examining old assumptions. When we do so, we find that Wrinch did not miss by as much as her detractors perhaps implied. With a little more luck, she might have gotten it right. Science is a bit like that, you need a dose of luck sometimes!
Tags: Cambridge, chair, Derek Barton, Dorothy Wrinch, energy, high energy species, Historical, mathematician, organic chemist, Patrick Coffey, relative free energy, thermodynamics, Tutorial material
A postscript to this post. In 1936, Dorothy Wrinch suggested a model for how proteins adopt rigid 3D structures. She was almost entirely wrong. The person who got it (almost entirely) right was Linus Pauling in 1951 (DOI: 10.1073/pnas.37.4.205). But he was wrong in one aspect; the handedness of the protein α-helix structures he was proposing, which came out left handed. Jack Dunitz (DOI) has written an article describing the background to this error. I mention this in the context of Watson and Crick, who employed very similar model building procedures to construct their own helical model of DNA. They got it right, but I venture to suggest mostly by luck rather than hard evidence. In the end, neither Pauling nor Watson and Crick suffered much from this looseness!
[…] why and how proteins fold continues to be a grand challenge in science. I have described how Wrinch in 1936 made a bold proposal for the mechanism, which however flew in the face of much […]