Henry Rzepa's Blog

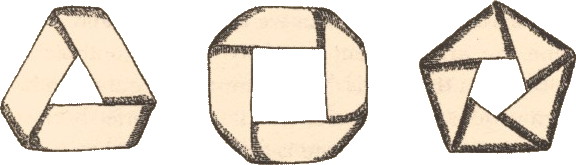
The Möbius band is an experimental delight. In its original forms, it came flat-packed as below. The one shown on the left is related to the international symbol for recycling (if we denote the number of half twists imparted as m, this one has m=3). The middle one (m=4) shows a 4-twisted variant, and the one on the right has a 5-twist (m=5). These all come from Möbius’ original sketches, found amongst his belongings when he died. In this post they will form the basis for some experiments in molecular chirality.

Flat-packed Möbius bands

These Möbius bands are all chiral, which means they cannot be superimposed upon their mirror image. We may in fact give the two forms labels, M and P (similar to the left and right handed helical forms for DNA noted in a previous post). Armed with a selection of these rings, I list below some experiments in paper cutting that you could try. I will use the notation M_m or P_m to denote the handedness and twistedness of each strip and + to denote glueing.

1. Build two strips, each m=1 and glue them together orthogonally, then cut down the middle of each strip with a pair of scissors. The process is already illustrated with lots of nice photos (using pink-coloured strips) on this blog and the outcome below is transcluded here from the original post. If the strips are flat-packed first, then they will fit into an envelope, and all that would be needed for the recipient to complete the valentine is the preceding instructions (plus some glue and scissors)!
   
2. My purpose here is to take this basic experiment and to suggest variations, using the following variables; the chirality M or P, the number of twists m in each, and the total number of strips used N. As is noted in the original instructions, a valentine is only produced if one M₁ and one P₁ strip is so joined (N=2), what chemists would call a heterochiral pair. What happens when a homochiral pair is used instead? The chemical term is that we end up with diastereomers, in other words M_1⁺P₁ and M_1⁺M₁ have a diastereomeric relationship, and P_1⁺P₁ and M_1⁺M₁ would have an enantiomeric relationship (as of course do M and P themselves).
3. One repeats experiments 1 and 2 using heterocoloured strips rather than the same colour as above. How are the two colours distributed?
4. Experiments 1-3 are then repeated for M₂ and P₂
5. Experiment 4 is then repeated for M₃ and P₃
6. One can now move on to N>2. For N=3, one might construct a isotactic polymer P₁+P₁+P₁ or a heterotactic polymer P₁+M₁+P₁.
7. The cutting down the centre of each strip does not have direct chemical analogy you might think, but in fact if you relate the cut to the node in a p-atomic orbital, one can quickly move into Möbius conjugation and aromaticity. One might ask whether any of the preceding experiments might relate to the molecular trefoil I described in another post? Or these lemniscular octaphyrins?
8. There are other variations. Thus N=2 dimers constructed with dissimilar twists as P₁+P₃ or perhaps even P₁+M₂. I will not try to list all the permutations.
9. If your head is not yet swimming, consider a tetramer N=4, but now complete a second supercycle by joining the first band to the fourth.
10. And as a final flourish, is it possible to give the supercycle described in experiment 9 a twist before you join the ends together? Would it matter if that twist were M or P? Would it matter if N were even or odd?  The chemical analogy here of course is to cyclic (and supercoiled) RNA molecules, which are increasingly implicated in the transition from pre-biotic to post-biotic chemistry.

I have to confess I have not tried the majority of the above experiments myself! If anyone does and gets anything interesting, do tell. What I hope I have illustrated here is how these simple experiments in twisting, gluing and cutting simple strips of paper may actually tell us something about molecules and their polymers and perhaps life itself.

Tags: chemical analogy, chemical term, Möbius, pre-biotic, RNA, Tutorial material, Valentine

This entry was posted on Sunday, February 13th, 2011 at 11:53 am and is filed under General. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.