When Watson and Crick (WC) constructed their famous 3D model for DNA, they had to decide whether to make the double helix left or right handed. They chose a right-handed turn, on the grounds that their attempts at left-handed models all “violated permissible van der Waals contacts“. No details of what these might have been were given in their original full article (or the particular base-pairs which led to the observation). This follow-up to my earlier post explores this aspect, using a computer model.
The DNA model used here is shown above; in shorthand it is d(CGCG)2. A crystal structure reveals it to form a (non-Watson-Crick) left-handed helix. If you open the 3D model below (based on a ωB97XD/6-31G(d)/SCRF=water optimisation), some of the short van der Waals contacts are measured. Most are around 2.25Å and the shortest is 2.1Å. It is worth noting that WC note in their article that a distance of 2.1Å for the B-form is acceptable (p92, bottom) and not a violation. All twelve hydrogen bond lengths H…O or H…N are normal, with lengths around 1.8Å. Given that a H…H distance is at its most attractive at ~2.4Å, and plenty of H…H distances of ~2.1Å are known from the crystal structures of organic molecules, one might conclude that (for the CG base pair), their hypothesis that the Z-form could be eliminated was wrong.

The DNA duplex d(CGCG) showing a left handed helix with short H...H contacts shown. Click for 3D
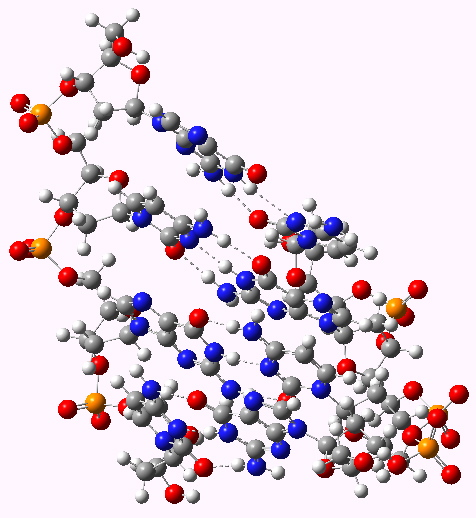
The DNA duplex d(CGCG) showing a right handed helix with short H...H contacts shown. Click for 3D
One crucial aspect of DNA is the local conformation about the bond connecting the base and the ribose, N9-C8 in the diagram below(green arrow).

Conformation of the base-ribose unit
What else can analysis of the wavefunction tell us? Well, curiously, the optical rotation of this particular small oligomer has never been reported in the literature, and an intriguing question is whether it might have proved useful to distinguish between B- and Z-forms of the duplex? To do this, one needs a reasonably reliable way of computing [α]D for both isomers. This is because optical rotations are not reliably additive, and it is difficult to estimate them accurately based purely on the fragments present in the molecule. In 2011, is is now perfectly possible to calculate this quantity quantum mechanically, even for 250 atoms, using a reasonable basis set and making allowance for solvation (which is known to affect the calculated rotation). The values (CAM-B3LYP/6-31G(d)/SCRF=water) for the Z-isomer are 66° and 32° for the B-isomer. Of course the model is not complete, lacking a counterion for the phosphate and explicit water molecules, but even so, it might appear that the reason optical rotations are not reported is that they truly are not useful!
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
Tags: B-DNA, computing, conformational analysis, dispersion energy, DNA duplex, interaction energy, optical rotation, van der Waals, Z-DNA
[…] the chiro-optical properties might be calculated (see DOI: 10.1002/chir.20804), including the optical rotation at a specified frequency, or e.g. the electronic circular dichroism spectrum. Such properties are normally computed only for […]
I wrote in this post that “plenty of H…H distances of ~2.1Å are known from the crystal structures of organic molecules”. Of course, distances to H in crystal structures are notoriously unreliable. Their actual positions are rarely optimised, but they simply ride on other atoms (e.g. C). The groups they ride on are often disordered, which makes distances even less reliable. With all these caveats, a search of the Cambridge database for intramolecular CH…HC contacts (with at least 5 intervening bonds) between 1.5 and 1.7Å reveals 2517 hits. It seems probable that the vast majority of these are artefacts, but I note just one, WALFOE (a twistane) for a particular reason. It was synthesized precisely to see just how short an intramolecular CH…HC contact could in fact be made. It is around 1.85Å. It may be unfavourable, but it does not make the synthesis of the molecule particularly difficult. An intermolecular search reveals 1628 hits. Shown below is the distribution of these latter hits, showing an intriguing maximum at ~1.6Å.
At the suggestion of Andrew White, our crystallographer, I have repeated the (intermolecular) search above, but specifically excluding any structure with disorder. This reduces the number of hits to 613. The histogram of H…H contacts is shown below.
The anomalous peak at 1.60Å is still there, with around 180 hits.
The process of optimising a molecule with 250 atoms is a slow one, and it is not obvious how stringent the criteria for a final geometry should be (it depends how shallow the potential surface is). So I should add that in the last week or so, further optimisation cycles have been applied to both the Z- and B-forms which has altered some of the hydrogen bond lengths (the geometries in the post have been updated with these more refined geometries). When the optimisation is finally complete, a free energy will be calculated and reported here.
[…] helix (and its further folding into a superhelix) might depend on the finely tuned properties of just one single bond in the […]
[…] upon their mirror image. We may in fact give the two forms labels, M and P (similar to the left and right handed helical forms for DNA noted in a previous post). Armed with a selection of these rings, I list below some experiments in […]
[…] thermodynamic energies of left and right handed DNA. In this earlier post, I noted some aspects of the calculated structures of both Z- and B-DNA duplexes. These […]
You can find a follow up discussion of some of the themes raised on this post at 10.1186/1758-2946-3-46 or here or on this blog post.