Henry Rzepa's Blog

Lactide is a small molecule made from lactic acid, which is itself available in large quantities by harvesting plants rather than drilling for oil. Lactide can be turned into polymers with remarkable properties, which in turn degrade down easily back to lactic acid. A perfect bio-renewable material!

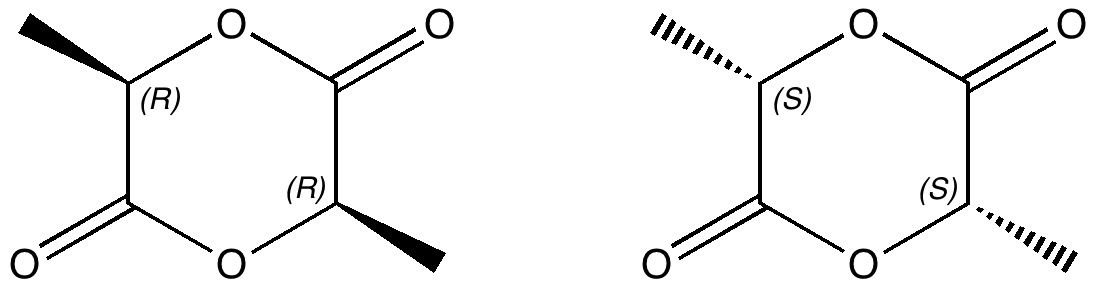
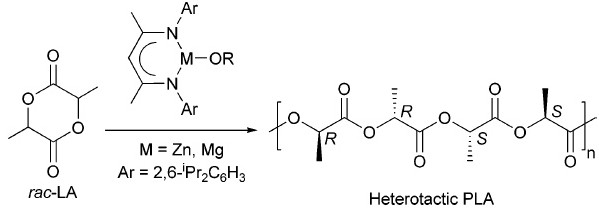
The starting point for ring opening polymerisation is racemic lactide, or rac-LA. This is an equal mixture of the R,R and S,S enantiomers, and it is now treated with a catalyst based on a metal M. If M=Mg, there is a rather remarkable stereochemical outcome for the resulting polymer. The catalyst selects alternating enantiomers for the assembly, resulting in a chain (R,R),(S,S),(R,R),(S,S), etc, the name for which is a heterotactic polymer. It could instead have created a blend of equal proportions of (R,R),(R,R),(R,R) and (S,S),(S,S),(S,S) which is an isotactic polymer. Needless to say, these two polymers have quite different properties, and it very much matters which is formed. Without such a catalyst, a random atactic polymer is created rather than a stereoregular arrangement.

The question is how does the catalyst manage to assemble the polymer with such stereoinduction? The origins of this depend on a detailed understanding of the mechanism of the reaction, and in 2005 we suggested one which offered an explanation for the stereospecificity (see E. L. Marshall, V. C. Gibson, and H. S. Rzepa, DOI: 10.1021/ja043819b and an interactive storyboard).

The key features of this rational were:

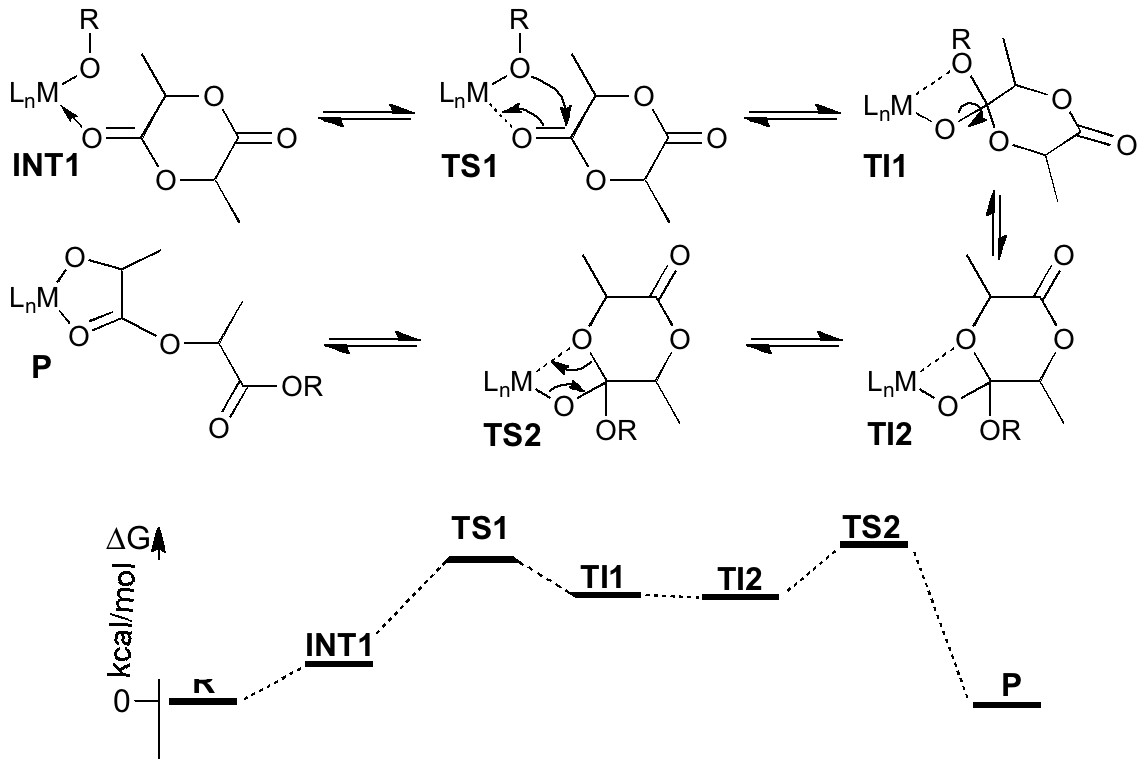
1. Two possible transition states may control the reaction, TS1 and TS2. Which one depends on which is the higher in energy.
2. The smallest model for this process involves loading two molecules of lactide onto the catalyst. The first has already been ring opened, and will control the stereochemistry of the second, which is the one suffering the ring opening bond formations/breakings shown above (the first is lurking in the group R).
3. This leads to four different possibilities, (R,R)-(R,R)*, (S,S)-(S,S)*, (R,R)-(S,S)*, and (S,S)-(R,R)* (where the * denotes the reacting lactide, as in the diagram above). These are all diastereomers, and hence will be different in energy. If one of the first two is the lowest, then isotactic polymer will result; if the latter two then a heterotactic polymer.

Back in 2004, we had constructed a model based on B3LYP and of necessity a mixed basis set, being 6-311G(3d) on the Mg, 6-31G on the lactide and only STO-3G on the catalyst. This was done because the complete system was actually rather large. Even so, a transition state calculation would regularly take at least 10 days to find using the fastest computers available to us at that time. Using this procedure, we found that the rate limiting kinetic step  was in fact TS2 for all four possibilities noted above. Of these, the (R,R)-(S,S) transition state turned out to represent the lowest energy pathway, thus confirming the observed heterotacticity for this particular catalyst.

Well, times have moved on:

1. Six years later, computers are around 20 times faster! We can now afford to improve the basis set to 6-31G(d,p) on all the atoms, including the catalyst (the Mg stays at 6-311G(3d) however; improving it to 6-311G(3d,2f) makes little difference).
2. We can now include the solvent (thf) as a continuum field.
3. In the last five years the B3LYP functional has been shown to underestimate the energies of globular molecules. A modern functional such as ωB97XD, which includes dispersion energy corrections, should be expected to do much better.

It is the purpose of this blog to report an update to the modelling. Quoting relative free energies (including the solvation correction), the results come out as;

1. (R,R)-(S,S) 0.0 kcal/mol for the TS1 geometry (see DOI: 10042/to-4950)
2. (S,S)-(S,S) 1.8 for the TS2 geometry
3. (S,S)-(R,R) 5.5 for the TS1 geometry
4. (R,R)-(R,R) 9.1 for the TS1 geometry.

Well, there are surprises! Using the gas phase B3LYP model the key transition state was TS2; now its TS1 (for in fact three of the four possible transition states). The bottom line (almost) is that the same stereoisomer as before comes out the winner! The take home lesson is that in six years of progress, modelling can now encompass solvent and dispersion corrections. Many mechanisms with > ~100 atoms investigated in the past without inclusion of these effects could probably do with a re-investigation, especially if the transition states are “globular” in nature. Any by now you are probably wondering what the transition state looks like. Well, here it is (and see it in all its glory by clicking on the diagram below).

And if you are also wondering how one might proceed to analyse the origins of the stereoinduction, the NCI interaction surfaces (as described in this post) are shown below. Note how the extensive degree of green interaction surface is associated with the globular nature referred to above.

Tags: 3g, animation, catalysis, chiroptical, dispersion energy corrections, E. L. Marshall, energy, gas phase, General, H. S. Rzepa, Interesting chemistry, Julia Contreras-Garcia, lowest energy pathway, oil, polymerisation, ring opening, V, V. C. Gibson

This entry was posted on Saturday, July 24th, 2010 at 8:50 pm and is filed under General, Interesting chemistry. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.