Following on from discussing octet expansion in species such as SeMe6, ClMe3 and ClMe5, I felt impelled to return to SF6, often used as an icon for hypervalence.
With this molecule we have twelve electrons to partition, six from sulfur and one each from six fluorines (the other six electrons on each F are presumed to form three sets of lone pairs). Recollect the two ways of dealing with them:
- To place them in pairs firstly into bonding MOs formed from using a 3s/3p valence atomic orbital basis on the S and a 2s/2p AO basis on F and to place any remaining electron pairs into antibonding orbitals constructed from the same basis. This would tend to reduce individual S-F bond orders.
- To place four pairs into bonding MOs and the remaining two pairs into MOs constructed using higher or Rydberg valence shells on S. This would tend to increase S-F bond orders by forming hyperbonds.
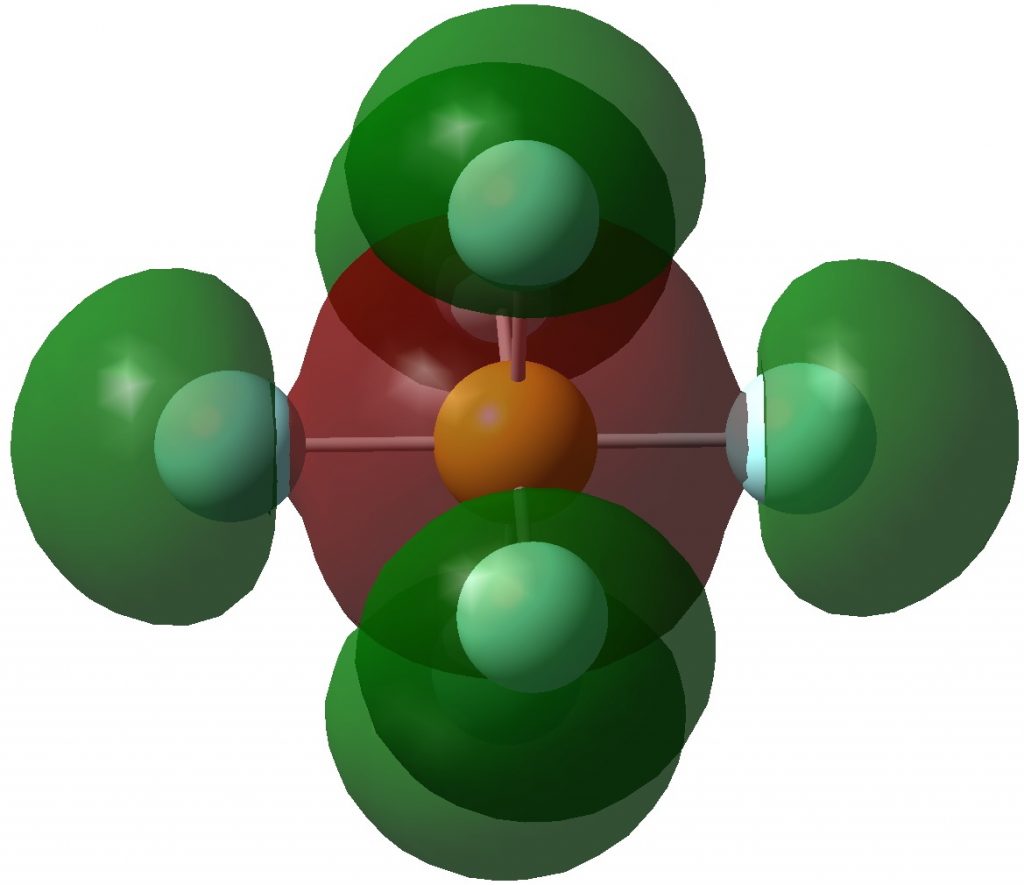
I will start with (delocalized) molecular orbitals (FAIR data DOI: 10.14469/hpc/3283). The HOMO (highest occupied MO) and the next 16 are in fact various variations of orbitals which can be regarded as fluorine lone pairs. The first of interest to us is the A1g-symmetric HOMO-17, which certainly looks as if it is antibonding along the six F-S bonds. But the heavy delocalization of the MOs makes it really difficult to comment on bonding/antibonding character.
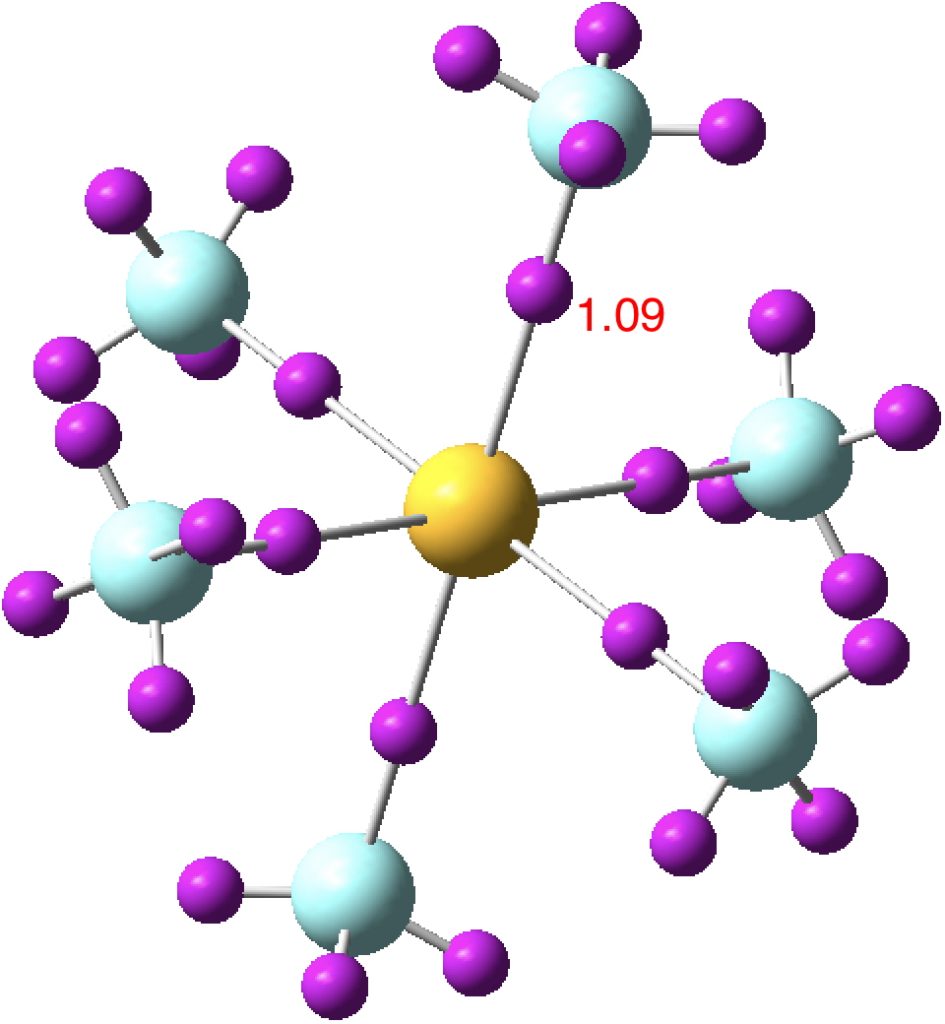
So next, the more localized NBO orbitals (FAIR Data DOI: 10.14469/hpc/3284), which tends to “collect” the wavefunction into localized regions of bonds and lone pairs. There are twelve equivalent F lone pairs of the following type: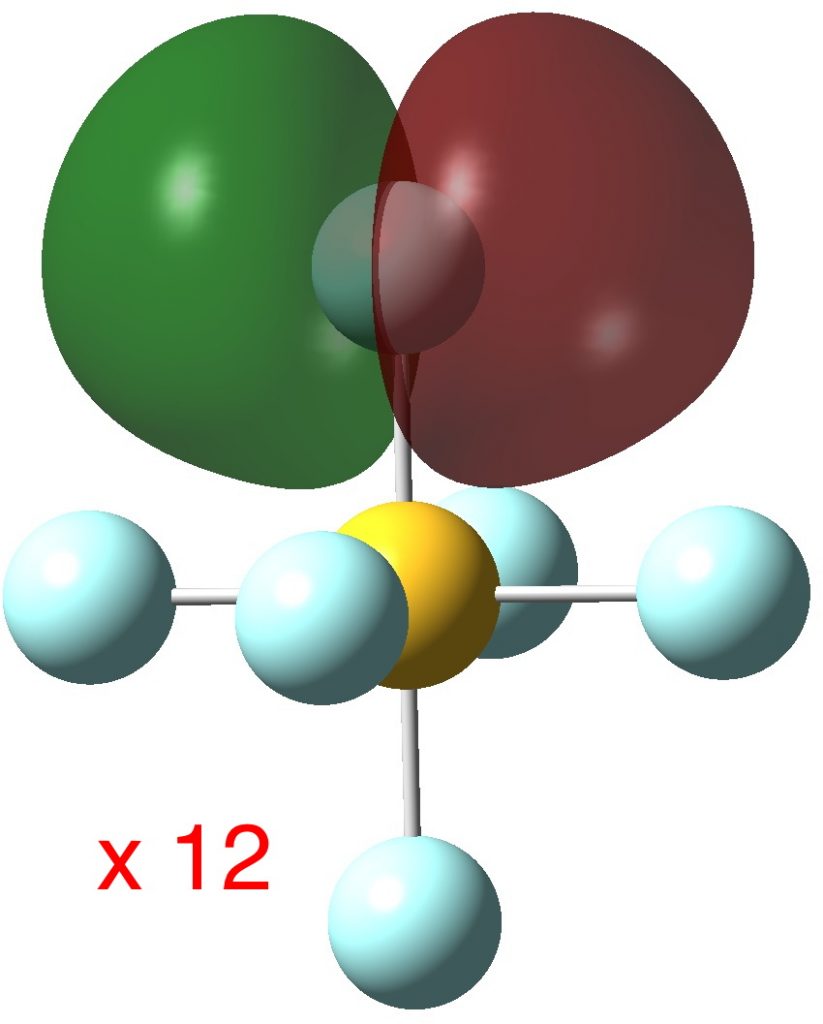
Next the remaining six F lone pairs, which are oriented axially along the S-F bonds. They have distinct S-F anti-bonding character.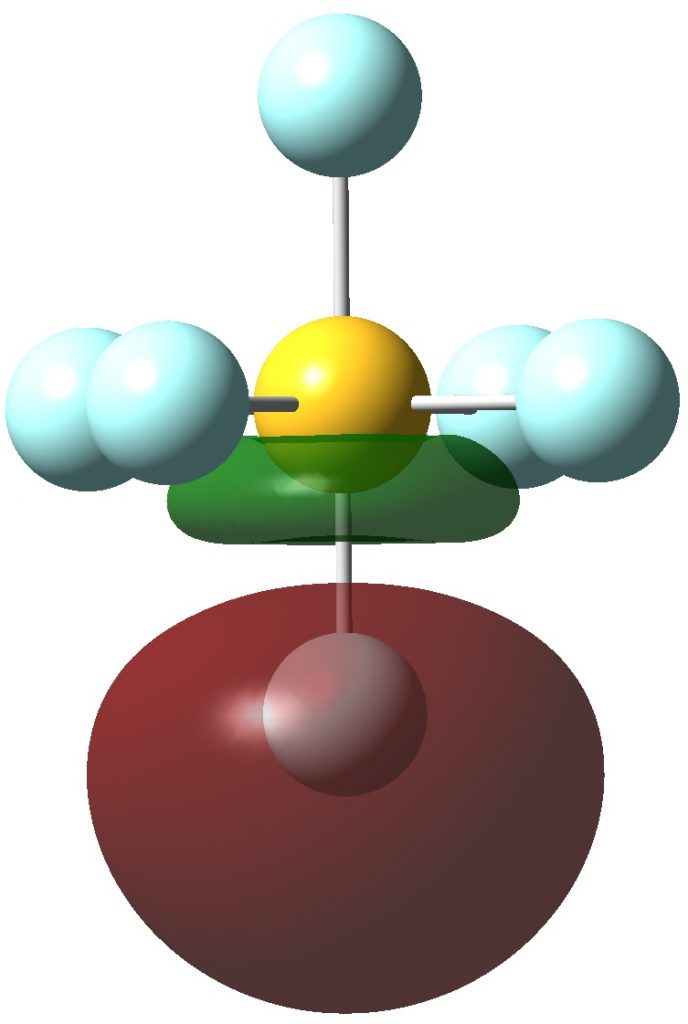
Finally six S-F bonding pairs (“acorn” orbitals). But note that whilst they are bonding along one S-F bond, they are mildly antibonding along the opposing S-F bond. 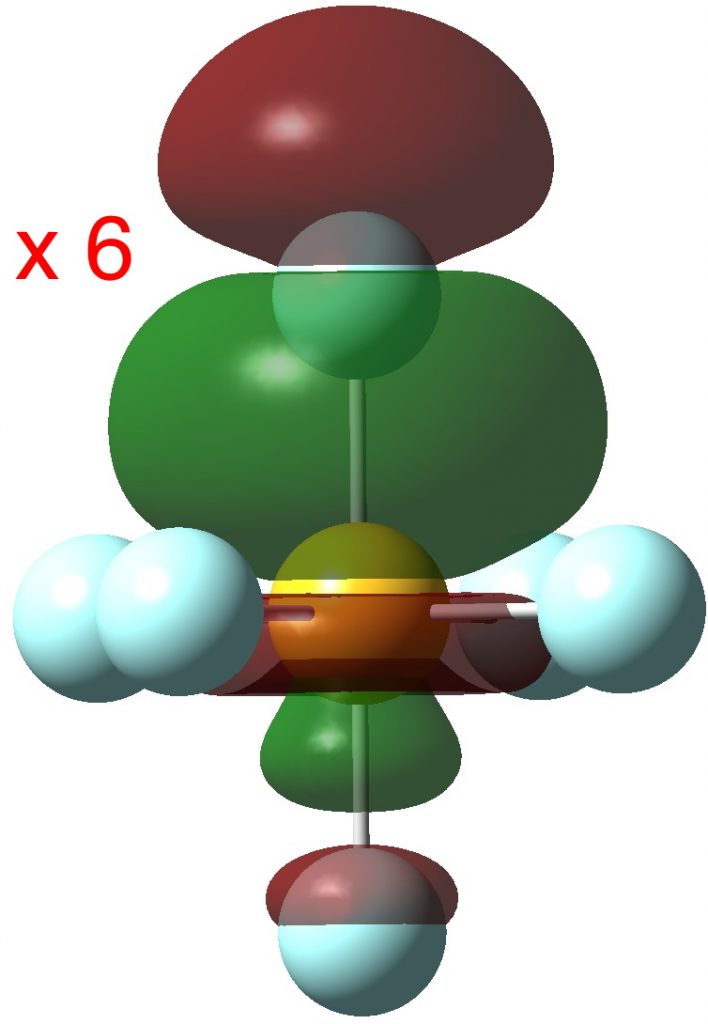
The Rydberg occupancy is S:[core]3S(0.98)3p(2.13)3d(0.24)4p(0.03)4f(0.01) and F: [core]2S(1.91)2p(5.51)3d(0.01), which gives a total Rydberg occupancy of 0.35177e. Adding up these effects, the NBO analysis tells us that the individual S-F bond orders are 0.7213. Six times this gives the Wiberg bond index at sulfur: 4.3276. This is close to the value of 4 expected from utilising an atomic orbital basis of one 2s and three 2p AOs on sulfur. One can think of this in another way.
- Start with a valence shell of twelve electrons to form six two-electron S-F bonds. The sulfur would have a bond index of six. Then promote either two electrons into fully antibonding orbitals (5-1=4) or four into non-bonding orbitals (F lone pairs) or possibly intermediate solutions, thus reducing the sulfur bond index by ~two bonds to give a bond index of four. Since the antibonding orbitals in this case are not fully antibonding, the bond index emerges a bit higher at 4.3276, a value also augmented by 0.35177/2 = 0.175885 due to Rydberg occupancy.
- One might usefully then ask if a bond index for sulfur of ≥ 4 can be usefully described as “hypervalent sulfur“? As usual in bonding theory, we need a reference state for non-hypervalent sulfur. If this is taken as two valencies, with a bond index of two, then this molecule is definitely hypervalent. If you assume that you can only construct the equivalent of four two-electron bonds using just a 3s1/3p3 atomic orbital basis, then it is merely mildly hypervalent; the four two-electron bonds are then distributed of course across six S-F regions, or 0.667 bonds per S-F region. The value of 0.7213 actually calculated is exalted by contributions in part from Rydberg orbitals.
What about the octet? 6*0.7213*2 = 8.66e, a mildly expanded octet. I am now going to use the ELF method as an alternative counting procedure. This is based not on orbitals but on the electron density (a more direct experimental observable than orbitals). Six disynaptic basins are located totalling 6.5e. The remainder of the electrons populate the F lone pairs shown below as four distinct monosynaptic basins per F. This is an artefact of the resolution of the cube of ELF values and how the basin centroids are located. These are in fact circular and not point ELF attractors, forming a circular ELF torus around each fluorine.
So, ELF suggests that the sulfur “octet” is not exceeded and in this form of analysis the compound is merely hypercoordinate. In contrast the orbital-based approach indicates mild hypervalency in which the total bond index at S modestly exceeds 4. If you regard the normal valency of sulfur to be two, this is clearly hypervalent. But no substantial octet-expansion beyond the modest Rydberg type is needed to rationalise this species and certainly not up to twelve!
Tags: chemical bonding, Chemistry, Hypervalent molecules, Octet, Sulfur hexafluoride
I believe the ELF approach is more accurate. This approach is in agreement with the respective electronegativities of the fluorine and sulfur atoms. The higher electronegativity of the fluorine atom would mean that the electrons in the S-F bonds are more localised on the fluorine atoms than the sulfur atom and hence, it is not surprising to find out that the number of electrons around the sulfur atom is, in fact, less than eight. Your calculations seem to be substantiated by this paper: DOI: 10.1021/ic011003v.
On a side note, I am rather interested in the topic hypervalency and would like to learn more about it. Do you have any books or articles to recommend? I would prefer a qualitative yet in-depth discussion because I do not have any knowledge of computational chemistry. Thank you very much!
One standard explanation for octet retention in say PF5 or SF6 is contribution from ionic structures such as eg PF4(+)F(-) or SF4(2+)2F(-), in which one or two electron pairs are localised into non-bonding F lone pairs. This is of course more or less what I meant in the text of my post, in which I discuss promotion of four of the twelve valence electrons into non-bonding orbitals.
Here is an unexpected result for OF6. I was anticipating this species to be a high order stationary point, with imaginary vibrational frequencies resulting in reductive eliminations of F2. But as this calculation shows (DOI: 10.14469/hpc/3760) it is actually a bona-fide minimum in the potential energy surface. The bond index at O is 3.44, which is significantly less than for SF6 and the Rydberg occupancies are low. So despite hypercoordination, it is definitely NOT hypervalent!
Here is one of the six O-F bonding NBO localized orbitals. Unlike the SF6 analogue, it has much more F-F bonding and hence less O-F bonding, which is why the oxygen bond index is reduced.
Here is NF5, also a stable minimum (DOI: 10.14469/hpc/3762 ). The nitrogen bond index is 4.043, and the two N-F NBOs are shown below. Note the F-F bonding in the first.
Have you looked into the perchlorate, perbromate, periodate series? I’ve never seen a satisfactory explanation of the bonding, or the reason for the stability of these ions. The oxides tend to be violently explosive. The salts are barely endothermic relative to loss of oxygen (probably only so due to lattice energies) and kinetically remarkably stable. The tetrahedral geometry at large central atoms appears superficially to militate against much O – O bonding. And the chemistry changes a great deal down the series.
These are indeed enigmas (see the post for perbromate). Stability is not just thermodynamic, it is also very much kinetic. To explore the latter, one needs to model all the possible decomposition pathways, which is absolutely non trivial. And as you say lattice energies probably play a big role.
So to answer this riddle will be non trivial.