This post arose from a comment attached to the post on Na2He and relating to peculiar and rare topological features of the electron density in molecules called non-nuclear attractors. This set me thinking about other molecules that might exhibit this and one of these is shown below.
The topology of the electron density is described by just four basic types, designed formally by the notation [3,-3], [3,-1], [3,1] and [3,3] and more colloquially by the terms nuclear attractor (NNA), line (or bond) critical point, a ring critical point and a cage critical point respectively. Mostly, the nuclear critical points coincide exactly with the actual nuclear positions, but more rarely these points are not found centered at a nucleus. It was such an NNA that was suggested as a comment on the post on Na2He. There I replied that another example of an NNA is to be found in H3+ and so its a short step to take a look at H42+ in a tetrahedral arrangement (DOI: 10.14469/hpc/2165). Since only two electrons are available for bonding, it is tempting to represent it as below, with dashed partial bonds connnecting the six edges of the tetrahedron and is associated with real normal vibrational modes; ν 416, 1490 and 1861 cm-1. A brief search on Scifinder, which appears to reference this species as hydrogen, ion (H42+), does not identify any publications associated with it (there are studies on H41+ however); if any reader here knows of any discussion please alert us!
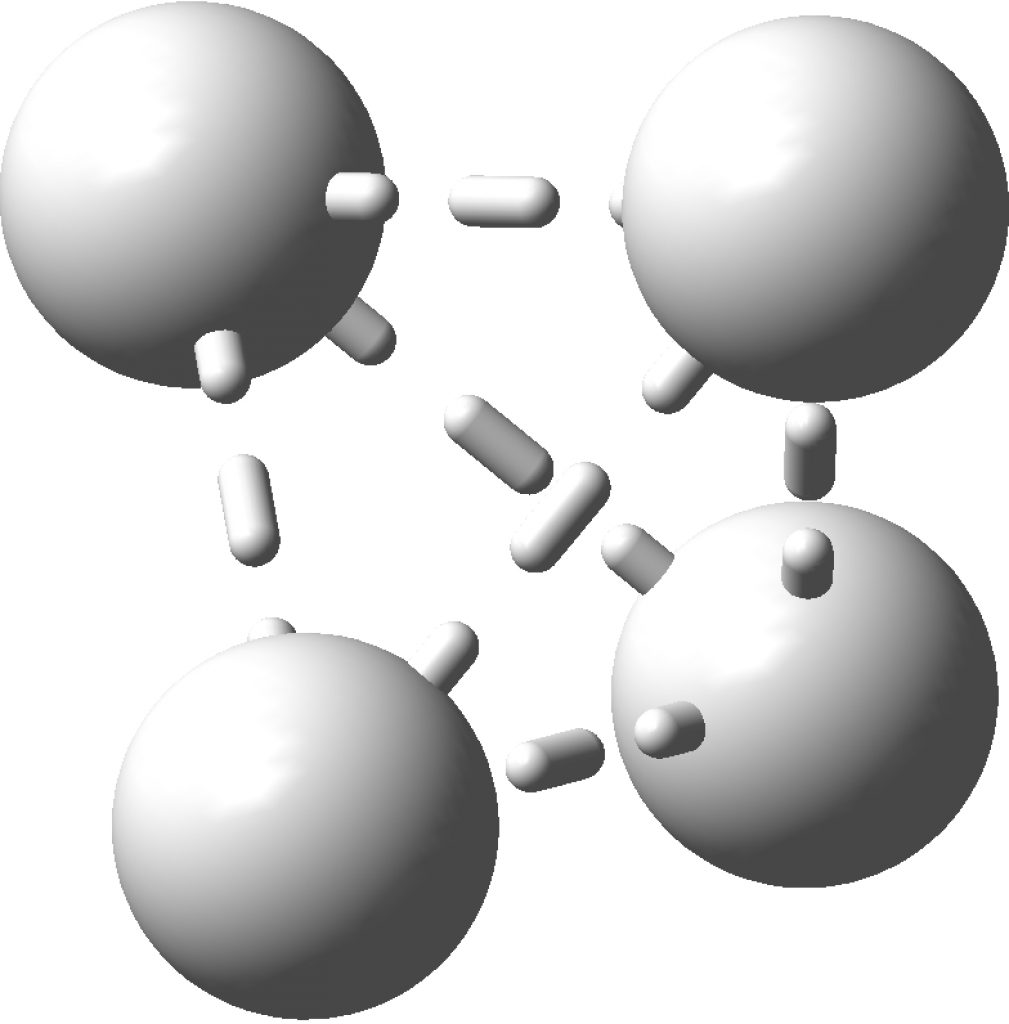
Analysing the density however gives a different result. A NNA is located at the centre of the tetrahedron and a line (bond) critical point connects this to each of the four hydrogen nuclei. This result is similar to the obtained for H3+. It is rather odd that these non-nuclear attractors have not entered into the vocabulary used to describe the bonding in simple molecules, but this picture is certainly different from the more empirical dashed lines between the four nuclei that one is instinctively drawn to use (above).
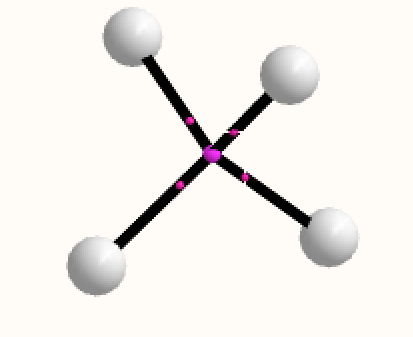
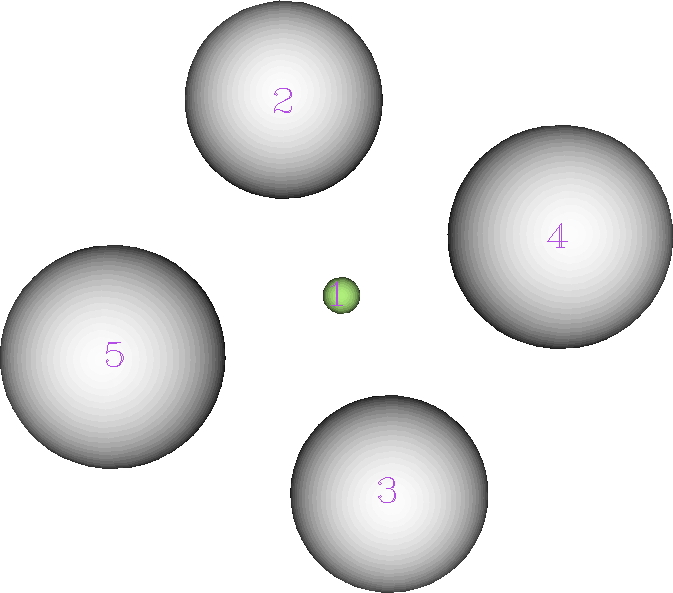
The ELF analysis (performed using multiWFN) is more interesting. The nuclear basins associated with the hydrogens reveal each has 0.425e, but the central one (green below) has its own basin with 0.301e.
The NICS value associated with the non-nuclear attractor is -27 ppm, which is indicative of strong spherical aromaticity.‡
All of which goes to show that even the simplest of molecular species may still have properties that are unexpected or certainly not well-known!
‡The H3+ species also has a non-nuclear attractor with a NICS value of -33ppm, this time two dimensionally aromatic (DOI: 10.14469/hpc/2653).
Tags: Attractor, brief search, Chemistry, Electron, Electron density, Hydrogen, Molecule, Nature, Physics, Quantum chemistry
Did you coerce the tetrahedral symmetry during the optimization? I’m attempting to optimize the structure myself, but the system explodes with both PBE0 and wB97X-D3 in ORCA 3.0.3. (From the trajectory, it looks like a hydrogen molecule ejecting two protons.)
I started from Td symmetry its true, but the end result (H…H separations 1.24Å) has only real force constants, with associated real vibrations. I used ωB97XD/6-311G(d,p). I did not investigate the thermochemistry with respect to any dissociated arrangements.
Ah, it appears the starting configuration is critical. When I use the coordinates from your input.gjf, the optimization goes smoothly to the geometry you describe.
Related paper:
M.N. Glukhovtsev, P.v.R. Schleyer, K. Lammertsma, “Can the H2+4 dication exist?” Chem. Phys. Lett., 1993, 209, 207-210. DOI: 10.1016/0009-2614(93)80094-6
(Answer: No)
See also
http://onlinelibrary.wiley.com/doi/10.1002/jcc.540140305/full
(Popular basis sets using the standard p exponent suggest (erroneously) that the Td geometry is a minimum)
Alex: The suggestion that basis sets can influence whether H42+ is a minimum or not is quite easily answered, since the system is so small! So I re-ran at the ωB97XD DFT level.
1. Def2-TZVPP (DOI: 10.14469/hpc/2181 ), ν +303, 1462, 1784.
2. Def2-QZVPP (DOI: 10.14469/hpc/2182), ν +173, 1466, 1779.
So probably at the CBS (complete basis set) limit, its probably a true minimum, but still worth testing!
But what about the Hamiltonian? The definitive test is CCSD(T).
3. CCSD(T)/Def2-TZVPP (DOI: 10.14469/hpc/2183), ν ~ -320i, 1460, 1835
4. CCSD(T)/Def2-QZVPP (DOI: 10.14469/hpc/2186), ν -325i, 1459, 1822.
So it seems its not the basis set but the Hamiltonian method that is sensitive. Such a big difference is a bit of a surprise; you would think that with just two electrons, a standard DFT method should not disagree so much with a coupled cluster method?
My purpose anyway was to explore unusual topologies in electron densities, and less to probe whether H42+ was a minimum or not.
One more basis: ωB97XD/aug-cc-pv6z (a 6-ζ level, DOI: 10.14469/hpc/2188) has ν 97, 1465 and 1780. So the CBS limit using this functional it probably is a real minimum.
I would add this is probably the largest basis set I have ever used in anger! I am also intrigued that the CBS limit is so difficult to reach!
Another: CCSD(T)/aug-cc-pv5z (DOI: 10.14469/hpc/2191) ∋ -325i, 1460, 1822 cm-1, which is pretty much basis-set converged.
Yet another Hamiltonian method, the CASSCF (complete active space self-consistent-field) procedure, which variationally optimises all the Slater determinants built from an active orbital space. The previous CCSD and DFT methods were based on just a single variational determinant.
CASSCF(2,5)/Def2-TZVPP (DOI: 10.14469/hpc/2203) ν ~+750, 1472, 1870 cm-1
CASSCF(2,8)/Def2-TZVPP (DOI: 10.14469/hpc/2205) ν ~+600, 1437, 1806 cm-1
This latter constructs 36 determinants based on 2 electrons and an active orbital space of 8, including 7 unoccupied orbitals. This recovers much of the so-called static correlation energy, but less of the dynamic version recovered by e.g. MP2 and CCSD methods. I will investigate these aspects next.
It is a feature of quantum chemistry codes that the same calculation can sometimes be requested by two or more relatively independent methods.‡ Whether they agree can serve as a check on both methods. In my previous addendum, I noted results for the CASSCF(2,5) method, citing the computed normal mode wavenumbers. By default, the code assumes that these will be calculated analytically.
An alternate way of calculating frequencies is by numerical differentiation and numerical second derivatives, which uses (in part) different code. Using this procedure one gets:
CASSCF(2,5)/Def2-TZVPP (DOI: 10.14469/hpc/2208) ν -307i, 1446, 1818 cm-1
CASSCF(2,8)/Def2-TZVPP (DOI: 10.14469/hpc/2211) ν -306i, 1446, 1818 cm-1
This compares with -320i, 1460, 1835 cm-1 obtained at the CCSD(T) level and same basis set. The initial conclusion is that the numerical set of results is more consistent with other methods than the analytical. The analytical frequency code is currently being inspected to try to identify the reason for the discrepancy.
There are in fact other anomalies. In any method which calculates the total energy of a system, one basic requirement is rotational invariance, which means that the energy must be identical no matter how the system is oriented for the calculation. One way of checking this invariance is to inspect the values of the six normal modes that represent the translations and rotations in a 3N second derivative matrix. For the numerical derivatives, these emerge as -32.6872 -32.5605 -32.3707 0.1435 0.2795 0.8246 cm-1, which is acceptable for this procedure. For the analytical version these are -0.0002 -0.0002 0.0002 515.2515 518.6620 518.8967 cm-1, with the last three clearly not being close to zero.
The various Hamiltonians do seem to be converging to the conclusion that this species is not a minimum, but a three-fold degenerate transition state for extrusion of H2 and two protons.
‡ The best test of course is to get the same result using entirely different codes. It can be fun setting everything up to do this, but with variational quantum chemistry codes it can be done!
Here is another take on playing with variational methods (DFT methods cannot be included in this game):
The total variational energies are obtained at the Def2-TZVPP basis set level:
1. CASSCF(2,5) -1.0440685
2. CASSCF(2,8) -1.0441268
3. CCSD(T) -1.0469931
4. CASSCF(2,5)/MP2 = -1.053945 Hartree. (DOI: 10.14469/hpc/2207)
The last of these, which includes both static and perturbational dynamic correlation energies, is clearly the lowest variationally. One more method, the multireference coupled cluster procedure, should give an even lower energy. I don’t have access to such code, but if anyone does, can they report that energy?