Nucleophiles are species that seek to react with an electron deficient centre by donating a lone or a π-bond pair of electrons. The ambident variety has two or more such possible sources in the same molecule, an example of which might be hydroxylamine or H2NOH. I previously discussed how for this example, the energetics allow the nitrogen lone pair (Lp) to win out over the O Lp. Here, I play a similar game, but this time setting an NLp up against a π-pair.
Before exploring this computationally, a reality check using measured crystal structures. Below is the search query used to explore the ability of the imine π-bond (the more novel or unusual of the two possibilities) to hydrogen bond to a proton as the model electrophile (see [1] for anther example of using this as a probe).
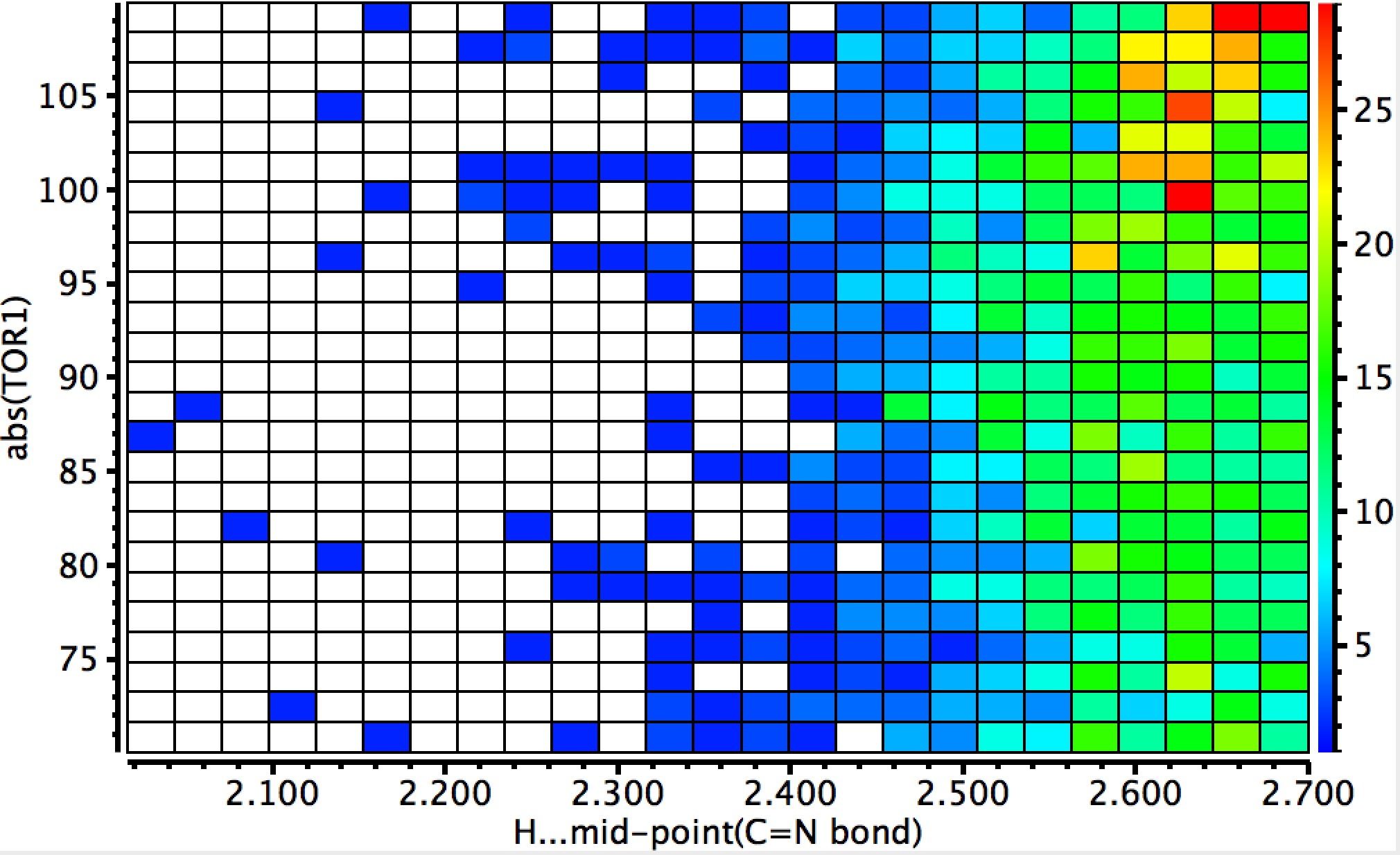
DIST1 is the distance from a hydrogen to the mid-point of the C=N bond (set to be in the range 1.8-2.7Å, the latter being shorter than the combined van der Waals radii of the atoms). The torsion is set to |70-110|° to restrict the approach of the hydrogen to above or below the π-bond. The usual no errors, no disorder, R < 0.05 and H-positions normalised applies. Some 2501 hits for intermolecular approaches closer than the van der Waals contact are found, with one hot-spot at a distance of 2.65Å and a torsion of ~100°. There is of course a continuum between a hydrogen bond and a dispersion attraction, but this plot shows there to be a fair few examples at distances of 2.4Å, a shortening which is normally taken as a hydrogen bond rather than a dispersion mode.
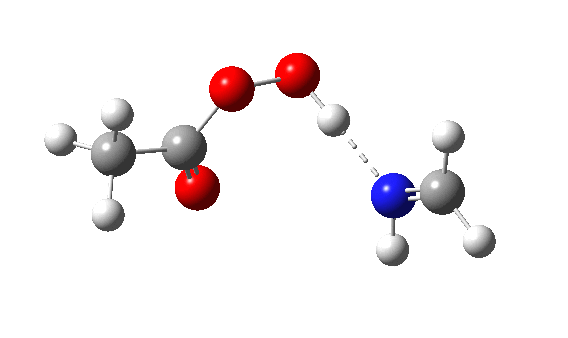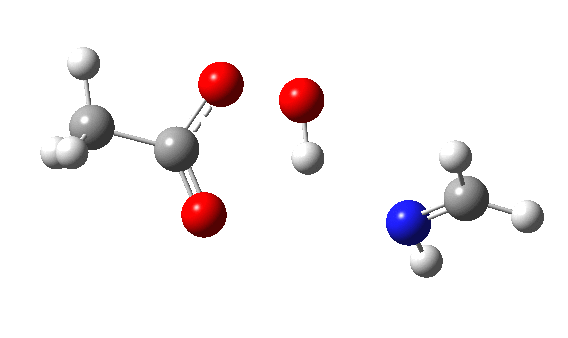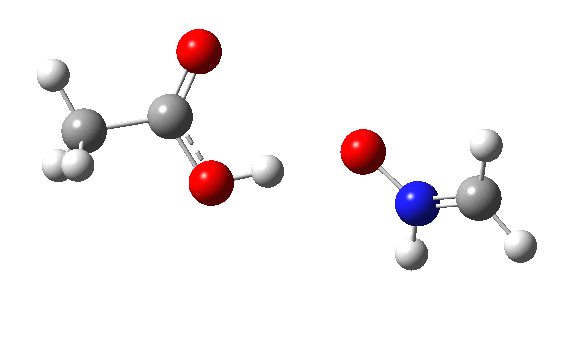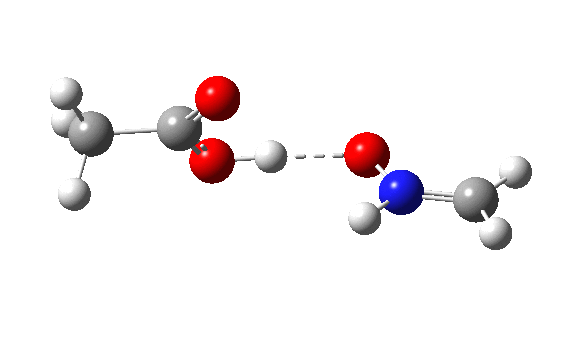
Using a simple imine as the nucleophile and a peracid as electrophile,[2] ωB97XD/Def2-TZVPP/SCRF=dichloromethane calculations (Nlp[3],Nπ[4]) reveal the Nlp barrier to be 16.2 kcal/mol lower in free energy (ΔG298) than Nπ. The normal explanation is that a Lp is bound only to a single nucleus, whereas a two-centre bonded pair is attracted to two nuclei. The means that the former therefore is more readily “available” to donate to an electrophile, by apparently 16.2 kcal/mol.
The IRC energy profile[5] for Nlp as a σ-nucleophile is shown below, with a relatively reasonable thermal barrier to reaction. The feature at IRC = 2 is in fact the proton transfer, which occurs only after the transition state has been passed. This behaviour was noted previously for the reaction of ethene with peracid, as verified experimentally by the measurement of kinetic isotope effects.
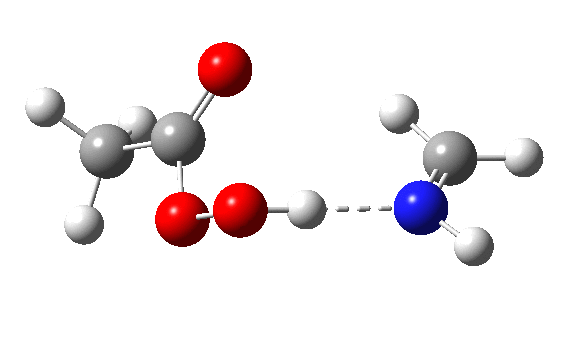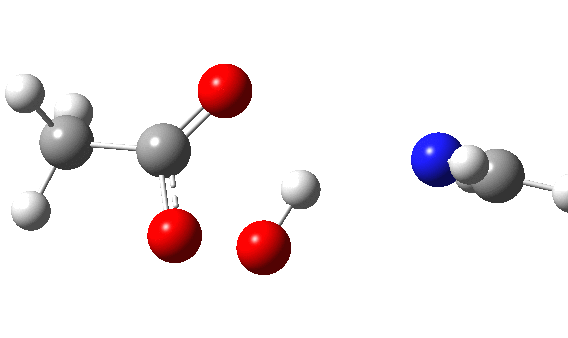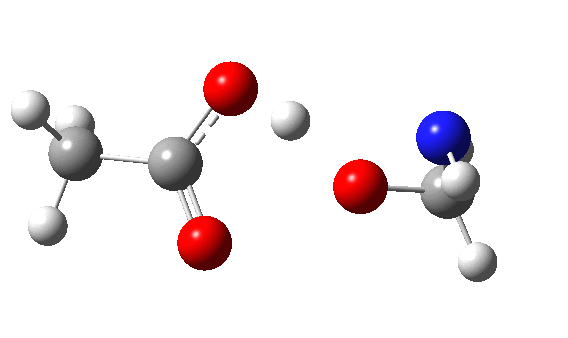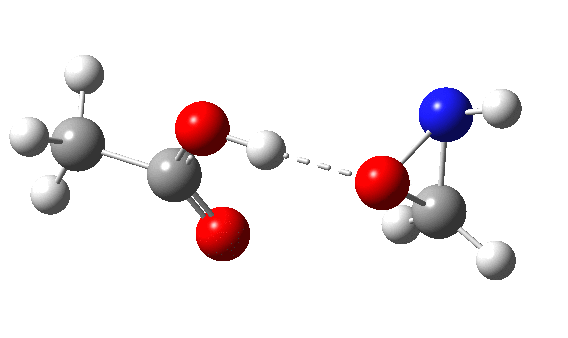
The π-nucleophilic route is shown below.[6] Note the higher barrier and the greater synchrony between the oxygen transfer and the proton transfer.
This leaves us with something of a problem. According to the literature,[2] the balance between σ or π is very even for the reaction between a peracid and an imine. For an aryl substituted imine, the proportion of the two products changes from 0% N (nitrone) and 100% π (oxaziridine) to 78% N and 22% π simply by changing the nature of the substituent. To achieve what is often referred to as 100% selectivity (normally understood as the minor isomer being <1% of the formed products) takes a free energy difference of ~2.7 kcal/mol (in fact ~RT ln 100/1), and a complete inversion is therefore ~5.4 kcal/mol. The computed difference of 16.2 kcal/mol is far too large to achieve such an inversion (substituent effects are rarely if ever of this magnitude). When faced with such a mismatch between experiment and computation, the explanation is normally because the modelled mechanism is the wrong one. So in this case, time to hunt for an alternative way of forming the oxaziridine. If I find a solution, I will update this post.
References
- H.S. Rzepa, "Discovering More Chemical Concepts from 3D Chemical Information Searches of Crystal Structure Databases", Journal of Chemical Education, vol. 93, pp. 550-554, 2015. http://dx.doi.org/10.1021/acs.jchemed.5b00346
- D.R. Boyd, P.B. Coulter, N.D. Sharma, W. Jennings, and V.E. Wilson, "Normal, abnormal and pseudo-abnormal reaction pathways for the imine-peroxyacid reaction", Tetrahedron Letters, vol. 26, pp. 1673-1676, 1985. http://dx.doi.org/10.1016/S0040-4039(00)98582-4