Ammonium hydroxide (NH4+…OH–) can be characterised quantum mechanically when stabilised by water bridges connecting the ion-pairs. It is a small step from there to hydronium hydroxide, or H3O+…OH–. The measured concentrations [H3O+] ≡ [OH–] give rise of course to the well-known pH 7 of pure water, and converting this ionization constant to a free energy indicates that the solvated ion-pair must be some ~19.1 kcal/mol higher in free energy than water itself.♣ So can a quantum calculation reproduce pH7 for water?
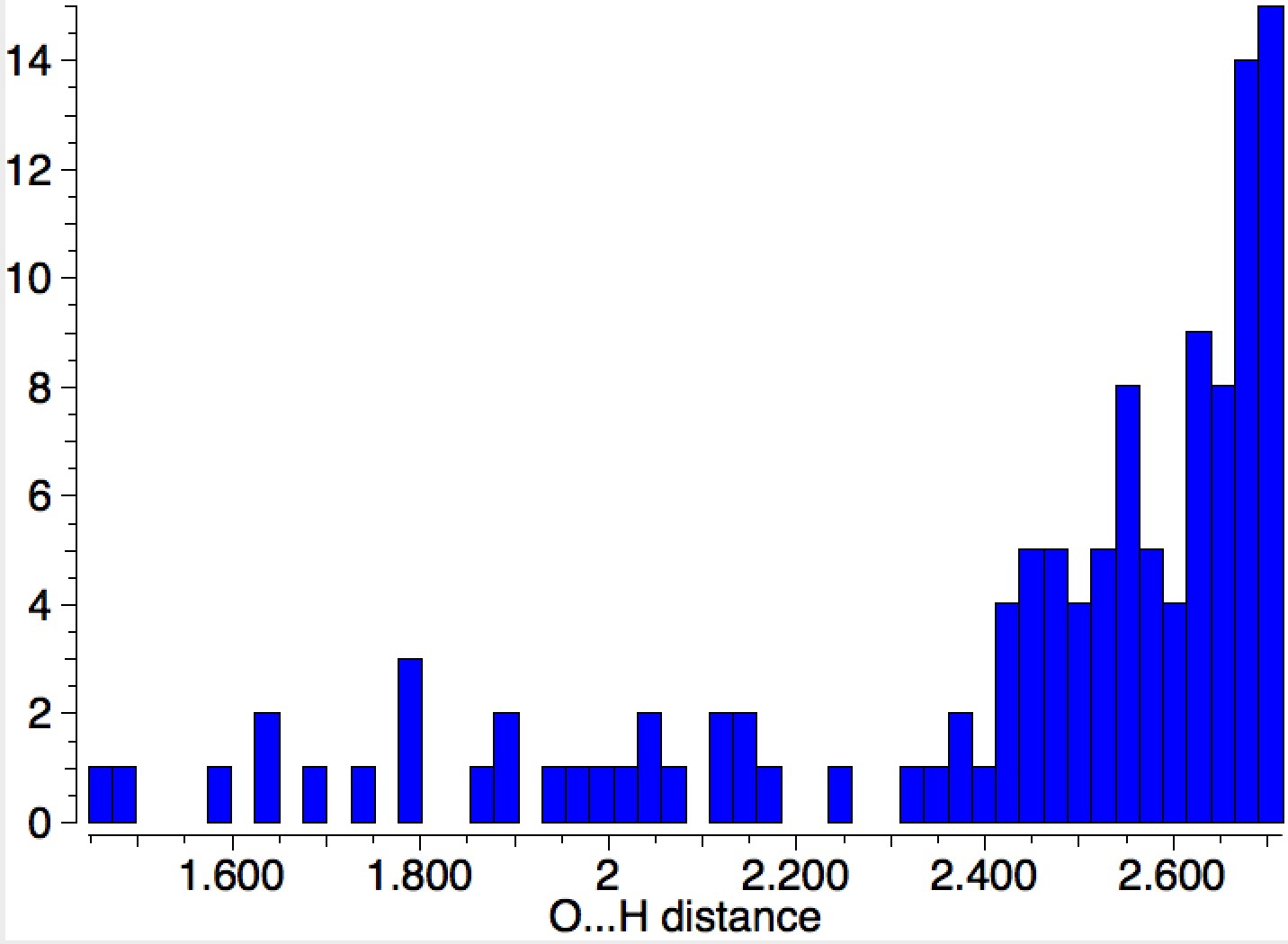
Let me start by saying that locating a stable minimum for H3O+…OH– is non-trival. I have been trying to find a structure on and off for a little while now, but all my erstwhile attempts have resulted in barrierless proton transfers back to H2O…OH2.† So I now decided on a more systematic approach by running a CSD (Cambridge structure database) search, defining the species H3O+ and specifying that the oxygen sustain one additional hydrogen bond, as per H3O+….H.[cite]10.14469/hpc/370[/cite] This produced 69 hits, with the distribution of O…H distances shown below indicating that a wide spectrum of hydrogen bond lengths to this oxygen appears possible.
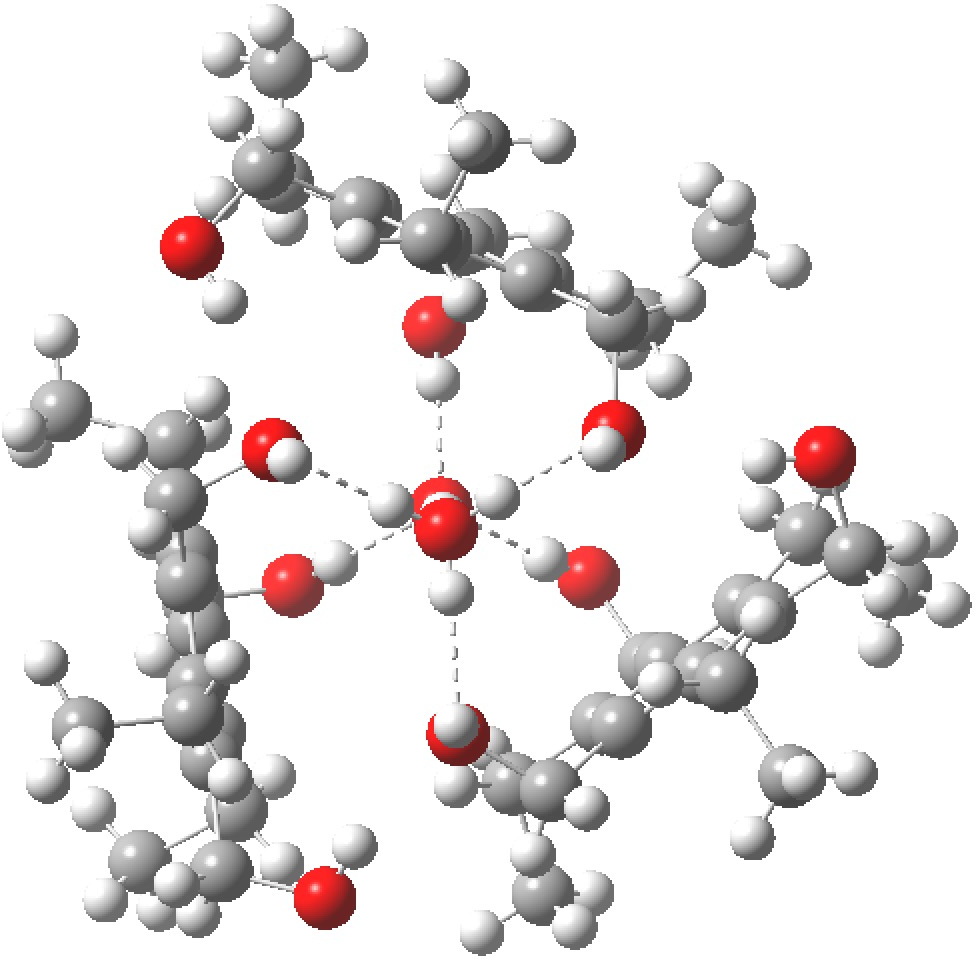
Restricting the search to H3O+….H-O and specifying that the last O is bonded to just one atom‡ reduces this to one hit.[cite]10.1002/chem.201406383[/cite] If you click on the image below or visit here[cite]10.5517/CC13Q0F8[/cite] you will see the hydrogen bonding pattern in this unique example is of the type (ROH…H)3O+…HO–(…HOR)3 with overall three-fold symmetry. The "bridge" across the ion pair in this case is formed from hydrogen bonds to -CH2OH groups in 1,3,5-tris(hydroxymethyl)-2,4,6-triethylbenzene.
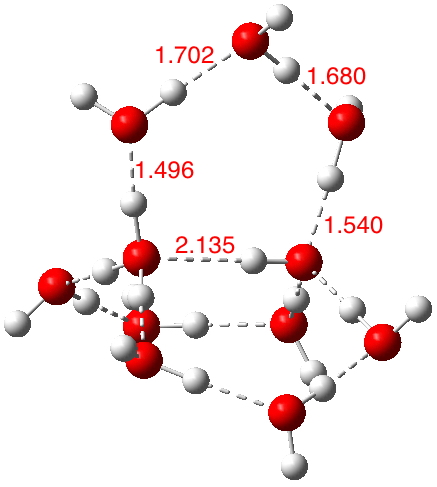
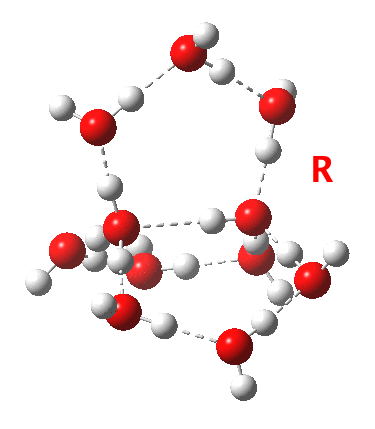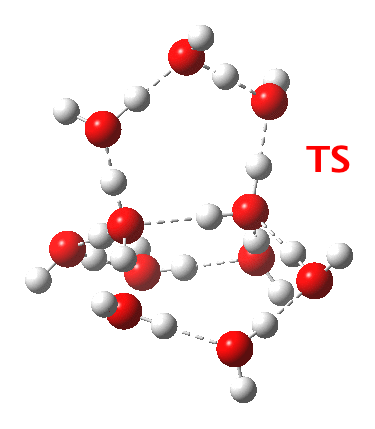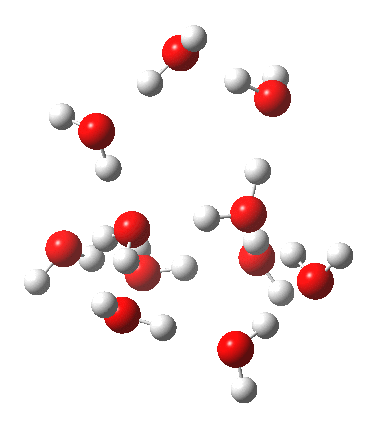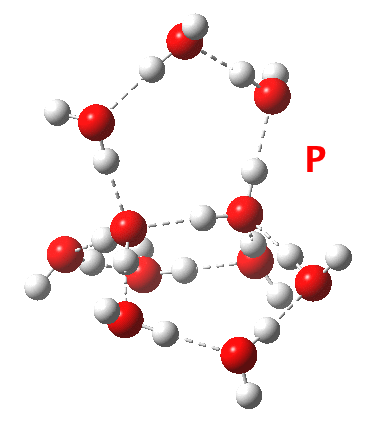
This structure immediately poses the question of whether water bridges could replace the organic bridge in the species above, to enable the elusive water-solvated hydronium hydroxide to finally be characterised as a bona-fide minimum in a quantum mechanical potential. By analogy one would need three bridges, each to be comprised of 3H2O. In other words a system containing eleven water molecules. An ωB97XD/6-311++G(d,p)/SCRF=water calculation indeed reveals this C3-symmetric arrangement is a minimum with a calculated[cite]10.14469/ch/191994[/cite] free energy (298K) 23.3 (23.5/Def2-TZVPPD) kcal/mol above that of the corresponding water cluster[cite]10.14469/ch/191995[/cite] in which a proton transfer has neutralised the ion pair. The error of +4.2 kcal/mol is probably due to a combination of incomplete basis set (calculations with better bases are under way), incomplete correction for solvation (continuum) as well as the limited size of the explicit water cluster (nine supporting water molecules) and other aspects such as the DFT method itself and the RRHO partition function approximations for thermal corrections. It would be a useful calibrant of all these aspects to explore whether these various corrections would converge to the known value or not.
The calculated geometry[cite]10.14469/ch/191994[/cite] reveals a H3O…HO hydrogen bond ~2.14Å, well within the range shown in the crystal structure distribution above.
With the basic model for hydronium hydroxide identified, one can now explore how to improve both the accuracy of the model in reproducing the "pH 7" observable and how indeed one might engineer a more superbasic variation.
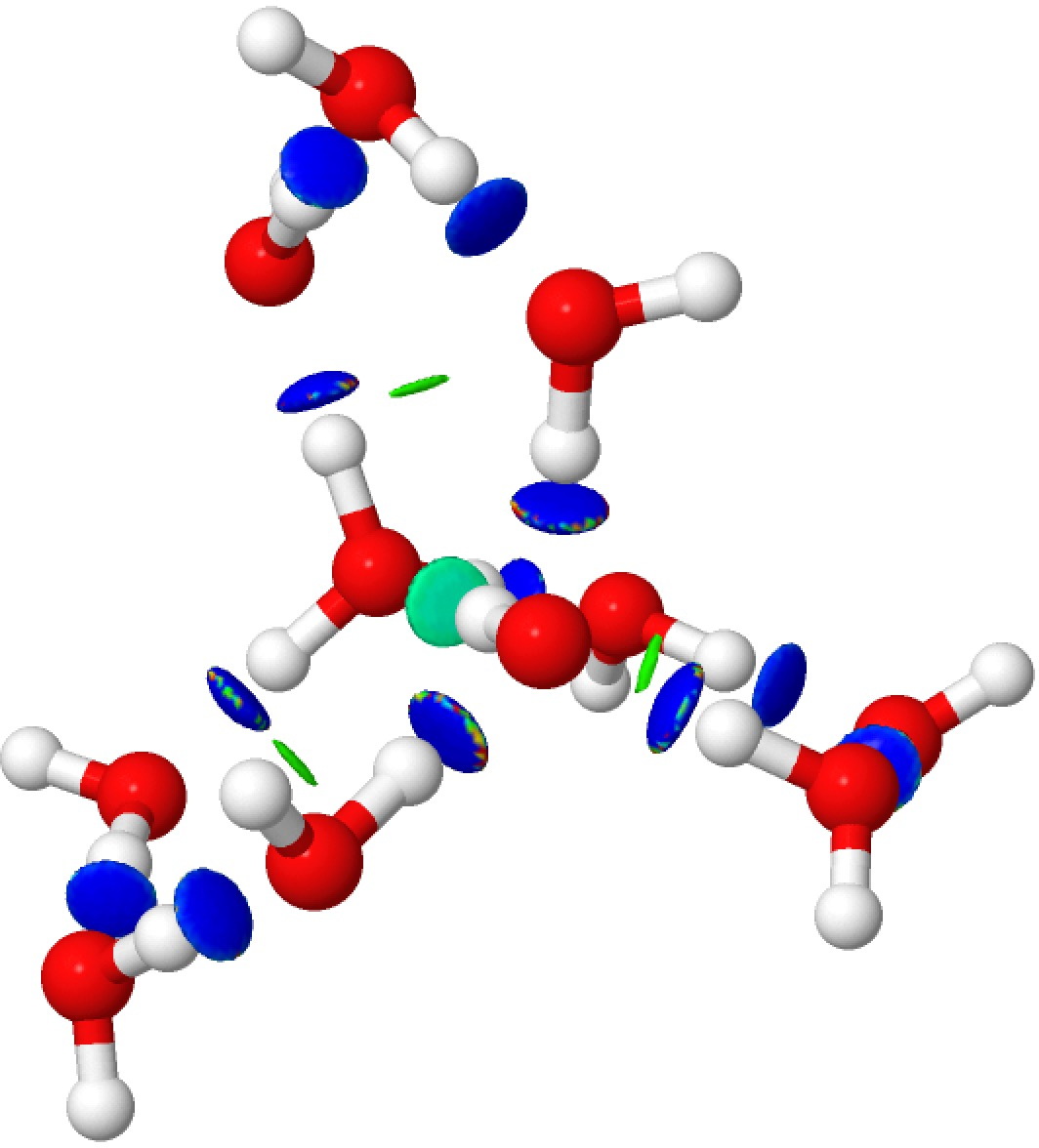
Addendum 1: The NCI (non-covalent-interaction) analysis of the hydronium hydroxide water complex is shown below. The blue regions indicate strong hydrogen bonds, with cyan being weaker. In fact, the covalent/non-covalent threshold normally taken for an NCI analysis (0.05 au) had to be increased to 0.10 for this example (the default threshold was already treating the HO…H interactions as covalent rather than non-covalent).
Addendum 2: Shown below is the intrinsic reaction cooordinate (IRC) calculated[cite]10.14469/ch/192002[/cite] for the proton transfer from the hydronium hydroxide ion-pair to form neutral water, revealing a barrier of ~3kcal/mol and exothermicity of 23 kcal/mol and how the dipole moment evolves.
♣Dissociation/equilibrium constants are rarely converted into free energies in text books and elsewhere. I would argue here that one gets a better intuitive feeling for such systems if expressed as energies. In this case, such a self-ionization energy for water might also be a useful way of calibrating how any given quantum mechanical procedure might perform in terms of the solvation model etc.
†Recent calculations of like-charge pairs of either H3O+ or OH– have been reported[cite]10.1039/C5CP02182K[/cite] but not as an ion-pair. The temperature dependence of the autoionization has also been reported[cite]10.1063/1.1878712[/cite] as involving, inter alia, changes in the coordination number of the OH– with temperature.
‡It is implicit when one talks about connecting bonds that the weaker hydrogen bonds do not qualify. Of course there is a whole spectrum of hydrogen bonding strengths; ones involved in ion-pairs for example can be up to 3 times stronger than those to neutral systems.
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
Tags: Acid dissociation constant, Acids, Cations, chemical bonding, energy, Equilibrium chemistry, free energy, Hydride, Hydrogen bond, Hydronium, Hydroxide, Physical chemistry, Properties of water, self-ionization energy, Self-ionization of water
This model has been updated to one with 12 solvent water molecules, distributed as three solvent bridges of four water molecules each. See 10.14469/hpc/8068.
The close ion pair is 1.1 kcal/mol in free energy higher than the fully separated ions, each solvated by 6H2O. Coulomb’s law suggests that separating the ion pair from ~3.3A to infinity will increase the potential energy by ~1.1 kcal/mol.
The separated ion pair is 23.3 kcal/mol higher than 14H2O itself.
I was reviewing chemistry and wondered about going from Kw to ΔE. I got 23.8 kcal/mol but i couldnt find any place confirming this wasnt nonsense. I tried using this value of ΔE to predict Kw at other T but it was far off. I had the idea of looking for a peak in the absorption spectrum (ΔE ~ 1.03 eV/pair ~ 1.3 um, NIR) but there seems to be none. Im not a chemist, just curious. Why isnt there a peak?
Dear pr,
The relationship is ΔG = -RT ln K. So two things there, need ΔG rather than ΔE and natural rather than base 10 logs. That should give the correct temperature dependence. The equilibrium does not involve electronic transitions. And the concentration of hydronium hydroxide is so small it would not register in any absorption spectrum.
Hope this helps.