This is the third and final study deriving from my Ph.D.[1]. The first two topics dealt with the mechanism of heteroaromatic electrophilic attack using either a diazonium cation or a proton as electrophile, followed by either proton abstraction or carbon dioxide loss from the resulting Wheland intermediate. This final study inverts this sequence by starting with the proton abstraction from an indolinone by a base to create/aromatize to a indole-2-enolate intermediate, which only then is followed by electrophilic attack (by iodine). Here I explore what light quantum chemical modelling might cast on the mechanism.
The concentration of I3– is used to follow the reaction, given by the expression: [I3–] = k1[B][indolinone]t – k-1/k2*ln[I3–] + const, where k2* = k2/715[I–] + k2' , the latter being the rate coefficient for the reaction between the enolate intermediate and I3–. With appropriate least squares analysis of this rate equation,‡ a value for k1 using either 1H or 2H (≡ D) isotopes can be extracted and this gives an isotope effect k1H/k1D of 6.3 ± 0.6. Note that this value does NOT depend on [B]. Here, I am going to try to see if I can construct a quantum mechanical model which reproduces this value.
- Model 1 uses just three water molecules as a proton relay (B3LYP+D3/Def2-TZVP/SCRF=water).
- Model 2 uses 2H2O.NaOH solvated by two extra passive water molecules. Since under these conditions, the NaOH is largely ionic, [B] ≡ [OH–]
| Model | ΔG‡298 (ΔH‡298) | kH/kD (298K) | DataDOIs |
|---|---|---|---|
| 1 | 28.0 (22.9) | 10.3 | [2],[3],[4] |
| 2 | 2.5 (2.8) | 4.4 | [5],[6],[7] |
The plot of rate vs [B] shows[1] that the uncatalysed (water) rate is very slow (intercept passes more or less through zero) and the calculated free energy barrier (28.0 kcal/mol) confirms a slow rate at ambient temperatures. Note in the final (aromatized) product, there is a noticeable hydrogen bond between the 3-carbon and a water molecule (2.14Å). The calculated kinetic isotope effect[8] is substantially larger than observed experimentally for the base catalysed contribution.
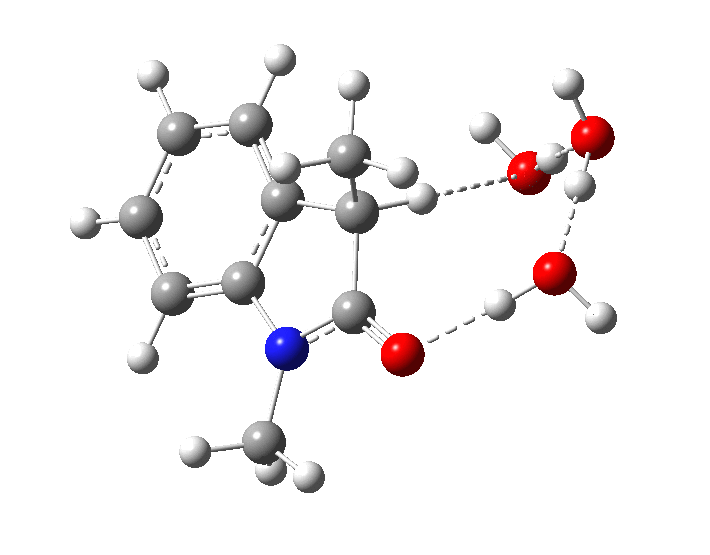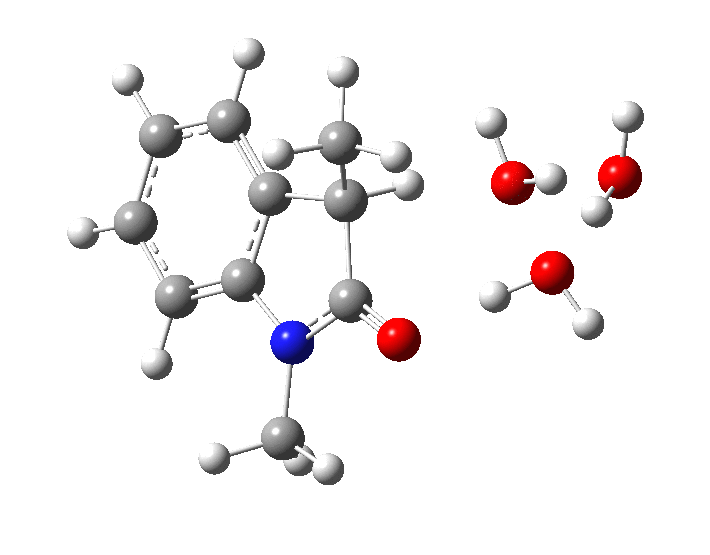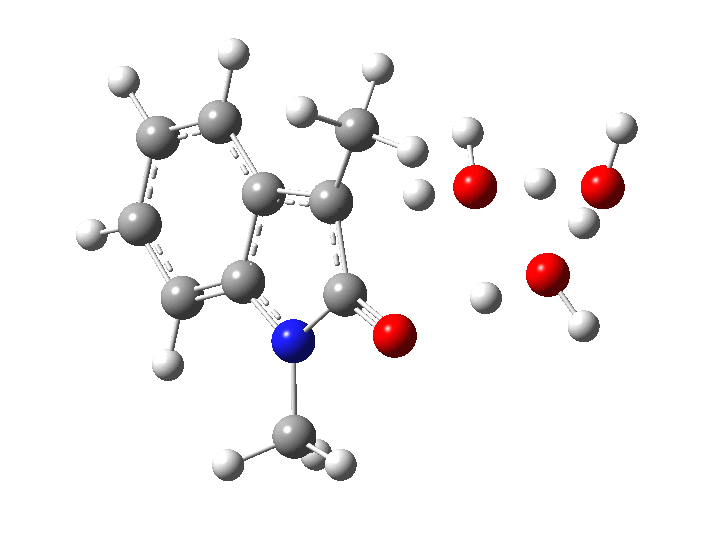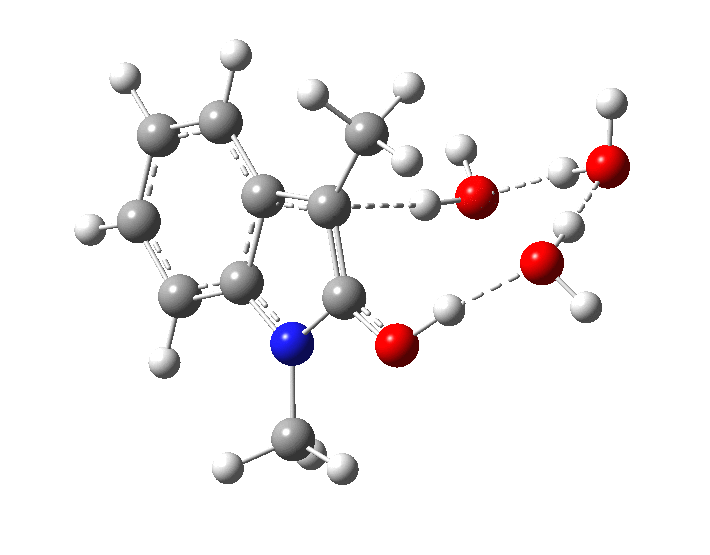
In the presence of NaOH (standard state = 1 atm = 0.044M), the enthalpy barrier drops very substantially to 2.8 kcal/mol and the free energy to 2.5 kcal/mol. Similar behaviour was noted previously on this blog for the hydrolysis of thalidomide. Although the magnitude of the reduction in barrier in fact implies an extremely fast reaction, recollect that [B]=[OH–] appears in the rate equation and since its value is very much less than 0.044M, the observed rate is relatively slow.
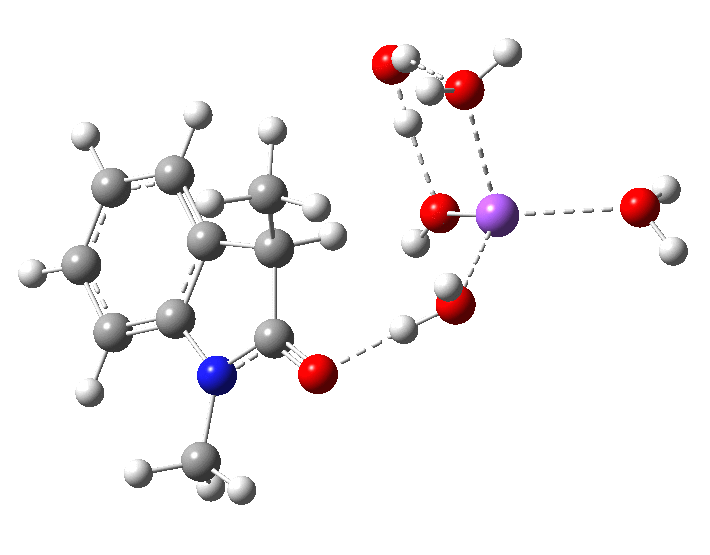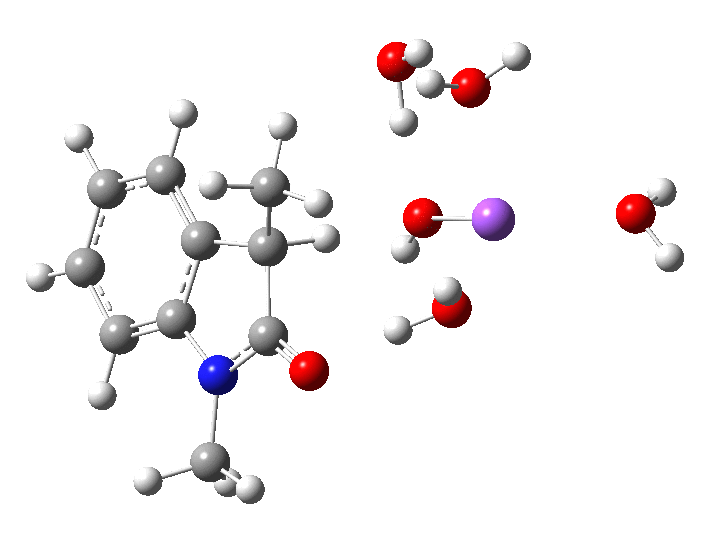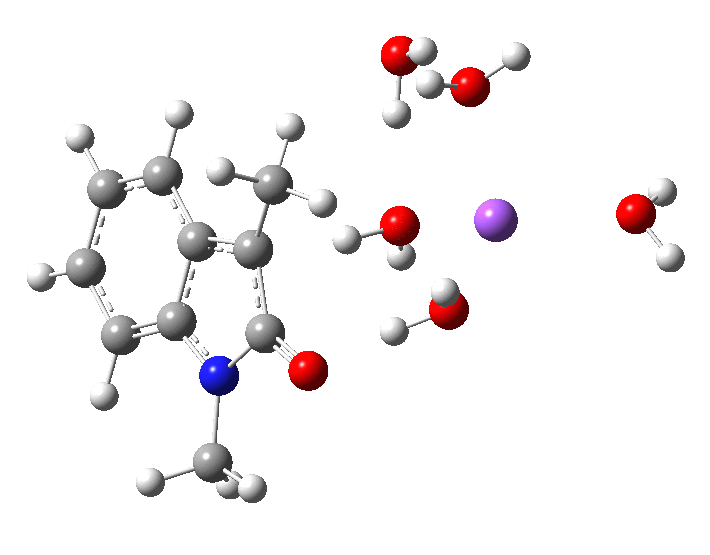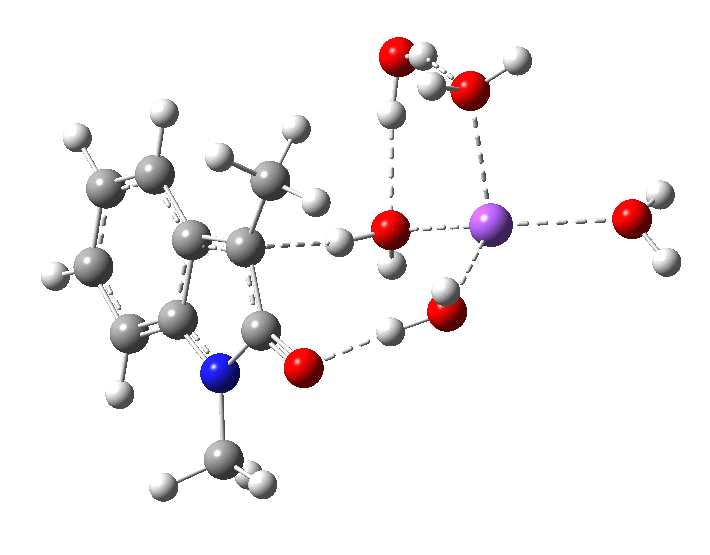
The calculated KIE for the hydroxide catalysed mechanism is much smaller that for the water route, but also smaller than is observed. This is a value uncorrected for tunnelling, which given the small barrier might be significant.
These calculations show how a model for ionization of indolinone can be constructed, and used to e.g. probe the sensitivity of KIE to perturbations induced by ring substituents, which may form the basis of a future post.
‡This is a non-linear equation with kinetics that straddle zero and first order behaviour. In 1972, it was not easily possible to graph such functions in a manner where the slope of a linear plot would yield the rate constant. It was only computers and languages such as Fortran which allowed such non-linear least squares analysis of the rate. In the event, it turned out that the presence of 50% methanol in the mixed aqueous solutions was the cause; in other solvents the kinetics approximated zero order behavour very well.
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
References
- B.C. Challis, and H.S. Rzepa, "Heteroaromatic hydrogen exchange reactions. Part VIII. The ionisation of 1,3-dimethylindolin-2-one", Journal of the Chemical Society, Perkin Transactions 2, pp. 1822, 1975. https://doi.org/10.1039/p29750001822
- H.S. Rzepa, "C 10 H 17 N 1 O 4", 2016. https://doi.org/10.14469/ch/191786
- H.S. Rzepa, "C 10 H 17 N 1 O 4", 2016. https://doi.org/10.14469/ch/191765
- H.S. Rzepa, "C10H17NO4", 2016. https://doi.org/10.14469/ch/191784
- H.S. Rzepa, "C 10 H 20 N 1 Na 1 O 6", 2016. https://doi.org/10.14469/ch/191787
- H.S. Rzepa, "C 10 H 20 N 1 Na 1 O 6", 2016. https://doi.org/10.14469/ch/191782
- H.S. Rzepa, "C10H20NNaO6", 2016. https://doi.org/10.14469/ch/191785
- H. Rzepa, "Mechanisms and kinetic isotope effects for the base catalysed ionisation of 1,3-dimethyl indolinone.", 2016. https://doi.org/10.14469/hpc/202
Tags: Arenium ion, Bases, diazo, Diazonium compound, Electrophile, Electrophilic aromatic substitution, Equilibrium chemistry, Fortran, Indole, light quantum chemical modelling, Metal ions in aqueous solution, Nuclear physics, Simple aromatic rings, Solutions