Another mechanistic study we started in 1972[cite]10.1039/P29770000281[/cite] is here 40+ years on subjected to quantum mechanical scrutiny.
The kinetics are again complex, the mechanism involving protonation‡ of the indole carboxylate (by a general acid), followed by the presumption of a zwitterionic Wheland intermediate that then loses carbon dioxide in a second step (blue arrows). Kinetically indistinguishable is a concerted alternative in which both steps are conflated into a concerted but not necessarily synchronous process (red arrows). In 1972, this latter mechanistic alternative was never really considered, iin part because it was not easy to prove or disprove an asynchronous concerted route by experiment. A brief summary of the conclusions:
- The reaction was found to be catalysed by a general acid.
- But a residual rate at low acid concentration was measured, corresponding to catalysis by water as an acid (shown in the scheme above).
- A deuterium isotope effect of ~2.2-2.7 on the apparent protonation step was observed when the reaction was conducted in D2O rather than H2O (the disentangled complex kinetics yielded isotope effects for two other kinetic parameters as well, also in the range 2.0-2.6).
- The isotope effects were found to be insensitive to various substituents on the indole, leading to the final conclusion that isotope effects for proton transfer are little influenced by the symmetry of the process.
Here, I set out to test some of these forty-year old assumptions; in particular to see if a model can be constructed that reproduces the unusually low value of the primary deuterium kinetic isotope effect, since normally proton transfers to carbon sustain a value closer to 7.
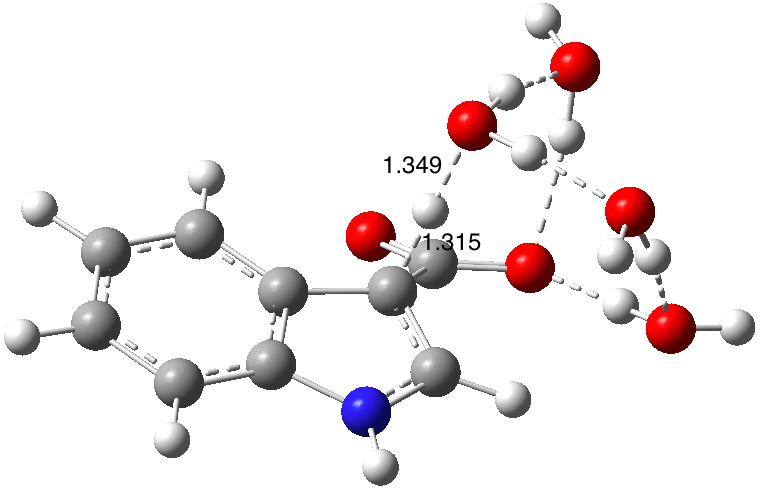
Now for the mechanism. Shown below are eight potential models for the process.
- Model 1 is the most basic, with just a single water molecule delivering a proton to the 3-position of the indole and abstracting it from the carboxylic acid group.
- Models 1a, 1b and 1c add a second water as a passive hydrogen bonder.
- Model 2 is isomeric to 1a,b,c but the second water now actively participates in the proton relay.
- Model 3 replaces the single water molecule with a more acidic proton relay molecule, ethanoic acid (red).
- Models 4 and 5 augment model 3 with one water molecule as well, in two different positions.
- Model 6 uses a three-water proton relay with one H-bonding water.
- Model 7 uses a two-water proton relay with two H-bonding waters.
The results of a B3LYP+D3/Def2-TZVP/SCRF=water calculation are collected below in the table. The following conclusions can be drawn:
- Model 1, with just a single water molecule acting as proton transfer acid/base reveals a concerted route via TS.
- Model 1b, with an extra water acting via a hydrogen bond now changes the mechanism to stepwise via TS1 and TS2, the latter being some 12.6 kcal/mol lower in energy and hence making TS1 rate determining. The kinetic deuterium isotope effect (KIE) on TS1 of 7.27 is much larger than is observed. That for the second step TS2 is negligible.
- Model 2, isomeric with 1b, is lower by 4 kcal/mol, largely due to a more favourable geometry for linear proton transfer. The KIE is getting closer to the observed value as is the free energy barrier (measured as ΔG‡298 22 kcal/mol[cite]10.1039/P29770000281[/cite]).
- Model 3 replaces the water proton transfer agent by ethanoic acid, with a significant lowering of the barrier. This constitutes a prediction for protiodecarboxylation in ethanoic acid solutions.
- Models 4 and the isomeric 5 now combines models 2+3, and represents one possibility for general acid catalysis in aqueous ethanoic acid solutions. The KIE is predicted to rise significantly (again, this experiment has not been done).
- Model 7 incorporates model 2 (a two-water proton relay) with two additional passive water molecules acting via hydrogen bonds. The barrier is converging to the measured value, and the KIE has now dropped below the measured value! As before TS2 is lower (by 6.8 kcal/mol) than TS1.
- Model 6 (below) is isomeric with model 7 and incorporates a three-water proton relay with one solvating water,† with a predicted KIE higher than model 6.
| Model | ΔG‡298 | dataDOIs | Mechanism | kH/kD [cite]10.14469/hpc/179[/cite] |
|---|---|---|---|---|
| 1 | 33.8 | [cite]10.14469/ch/191738[/cite],[cite]10.14469/ch/191728[/cite] | TS[cite]10.14469/ch/191735[/cite] | 9.88 |
| 1a | 35.6 | [cite]10.14469/ch/191737[/cite],[cite]10.14469/ch/191733[/cite] | – | – |
| 1b | 33.8 (21.2) | [cite]10.14469/ch/191737[/cite],[cite]10.14469/ch/191732[/cite],[cite]10.14469/ch/191748[/cite] | TS1,TS2[cite]10.14469/ch/191741[/cite] | 7.27 (1.05) |
| 1c | 33.9 | [cite]10.14469/ch/191737[/cite],[cite]10.14469/ch/191729[/cite] | – | – |
| 2 | 29.9 | [cite]10.14469/ch/191737[/cite],[cite]10.14469/ch/191731[/cite] | TS1,TS2[cite]10.14469/ch/191739[/cite] | 4.20 |
| 3 | 20.9 | [cite]10.14469/ch/191745[/cite],[cite]10.14469/ch/191743[/cite] | TS1,TS2[cite]10.14469/ch/191749[/cite] | 4.29 |
| 4 | 25.7 | [cite]10.14469/ch/191747[/cite],[cite]10.14469/ch/191734[/cite] | TS1,TS2[cite]10.14469/ch/191751[/cite] | – |
| 5 | 24.4 | [cite]10.14469/ch/191747[/cite],[cite]10.14469/ch/191742[/cite] | TS1,TS2[cite]10.14469/ch/191754[/cite] | 8.55 |
| 6 | 23.9 | [cite]10.14469/ch/191753[/cite],[cite]10.14469/ch/191755[/cite] | TS1,TS2 | 5.66 |
| 7 | 24.3 (8:17.9) | [cite]10.14469/ch/191753[/cite],[cite]10.14469/ch/191750[/cite],[cite]10.14469/ch/191752[/cite] | TS1,TS2[cite]10.14469/ch/191756[/cite] | 1.44 |
These models show that the arrangements of the solvation and proton-relay components of the mechanism are crucial to understanding the kinetic isotope effects induced by deuterium. The partition function ratios responsible for the KIE emerge[cite]10.14469/hpc/179[/cite] as a complex function of the structure and so the KIE itself provides a particularly sensitive probe of these structures. This exploration is not stochastical in nature; there are clearly many more variations in which even more than four water molecules could be used in the model. One would take the Boltzmann population/weight of each pose and use these to predict the statistical probability of properties such as the KIE. Working in the other direction and from the results shown in the table, a population of ~25% of model 6 and 75% of model 7 would give a KIE in agreement with experiment. A more complete stochastical model would no doubt include many more solvation structures.
In 1972, transition state models could only be slowly and painfully constructed by accumulating kinetic data and making many assumptions. Quantum computation provides a more systematic and rational way in which to base the assumptions. What has emerged for this reaction is that the rate determining protonation of a 3-carboxyindole prior to its decarboxylation is largely defined by the solvation structures that accumulate in the transition state; we are really learning about solvation here rather than just proton transfer. The two techniques together, experimental kinetics and quantum chemical modelling, are true symbiotes in each informing the other.
‡Here is a crystal structure which shows an O-H hydrogen bond to the π-face of the indole 5-ring, indicating the indole π-system is basic enough to hydrogen-bond with an acidic proton.[cite]10.5517/CC10K1M7[/cite] †This water molecule has an additional role, which I will describe in a separate post.
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
Tags: aqueous ethanoic acid solutions, energy, ethanoic acid solutions, free energy barrier , quantum chemical modelling