Sometimes you come across a bond in chemistry that just shouts at you. This happened to me in 1989[cite]10.1039/C39890001722[/cite] with the molecule shown below. Here is its story and, 26 years later, how I responded.
To start at the beginning, there was a problem with the measured 1H NMR spectrum; specifically (Y=H, Z=O) there are supposedly 16 protons, but only 15 could be located. What had happened to the 16th? To understand how one proton had been “lost”, you should appreciate that on most FT-NMR instruments, one has to specify a spectral window to collect data, and normally for protons, that window ranges from ~14 to -2 ppm. So the standard response to lost signals is to expand the window. When that was done, the offending proton appeared at 19 ppm! You should understand that this is an unusual chemical shift for a proton, and is normally taken as indicating very high acidity. But carboxylic acid protons are not regarded as particularly acidic? The mystery was resolved by recording the crystal structure at low temperatures, and this revealed that this hydrogen was (almost) symmetrically disposed between the oxygen and the nitrogen. The N-H distance was 1.32Å and the OH 1.17Å. Whilst such symmetric disposition is not that unusual between two atoms of the same type (O-H-O or N-H-N) it was quite unexpected between two different heteroatoms. And such symmetry alone is sufficient to induce very high chemical shifts; acidity per se does not come into it.
That bond clearly shouted at me; so much so that in the text of the original article, we wrote “it is interesting to speculate whether these characteristics could be fine tuned by modification of the pKa values with suitable ring substitution“. What I had in mind was whether the position of the H could be made perfectly symmetric by adjusting the substituents. But for 26 years this idea lay dormant. Until this post! Rather than make lot of compounds (1-3 years!) I will do it with (lots of) computation (2 days!!).
So to start we need a reality check. I am using the pbe1pbe/tzvp/scrf=chloroform method (this functional is often used for hydrogen bonds) and the collected results are shown in the table below.
- For Y=H, Z=O, the calculation predicts single minimum, with the hydrogen closer to O. Starting from an NH bound hydrogen ends with it on O. It is what is called a single well potential. The disposition of that H is not quite correct, but the computed 1H NMR shift is pretty close to experiment, and so I will take this method as reasonably good.
- With Y=Li, the polarisation of the N-Li bond enhances the basicity of the second N, and the H now ends up on this atom rather than O (even if it starts on O). Another single well potential. We now know that any symmetric species must occur somewhere between Y=H and Y=Li in terms of the electronegativity of the substituent Y.
- Unsurprisingly, Y=Na does not bracket Y=H/Li and the H moves even closer to the N. Again a single well potential.
- Y=Li.1H2O or 2H2O do not help either (surprisingly?)
- Y=BeH brackets Y=H/Li, but we also see new behaviour with a double-well potential; the H can be attached to either O or N and the former is slightly more stable by 0.22 kcal/mol in ΔG. The barrier is tiny, well below the energy of the first vibrational level, and so experimentally this system will manifest as the average of these two isomers and the H will similarly manifest with its most probable position being at the average of the two minima, N-H ~1.30, O-H ~1.3Å. Success! At this point, the NMR shift is at its greatest.
- Y=BH2 continues the trend as a double minimum, this time with the H-O species the more stable by ΔG 0.68 kcal/mol; we are now past the symmetric point.
- By Y=SiH3, the single-well minimum (with H-O) is restored and we emerge with the same result as Y=H.
- And to complete the scan, Y=H, Z=S is the same as Z=O.
- Some second order tuning can be tried by changing the substituent on Y=BeH to Y=BeF, again a double minimum with HO more stable than NH by 0.30 kcal/mol in ΔG, and with a ΔG298 barrier from O to N of only 0.02 kcal/mol! The fine-tuning is again towards symmetrisation.
I will stop at that point. Unfortunately of course the Y=BeF derivative is unfeasible synthetically and hence unlikely to be tested.
| Y | N-H, Å | O-H, Å | δ, ppm | FAIR Data Citation |
|---|---|---|---|---|
| H (expt) | 1.32 | 1.17 | 19.0 | [cite]10.1039/C39890001722[/cite] |
| H (calc) | 1.48 | 1.04 | 18.6 | [cite]10.14469/ch/189475[/cite] |
| Li | 1.06 | 1.52 | 16.5 | [cite]10.14469/ch/189475[/cite] |
| Na | 1.05 | 1.55 | 15.6 | [cite]10.14469/ch/189477[/cite] |
| Li.H2O | 1.06 | 1.52 | 16.6 | [cite]10.14469/ch/189478[/cite] |
| Li.2H2O | 1.06 | 1.52 | 16.6 | [cite]10.14469/ch/189480[/cite] |
| BeH | 1.11 | 1.39 | 20.6 | [cite]10.14469/ch/189476[/cite] |
| BeH | 1.49 | 1.04 | 18.7 | [cite]10.14469/ch/189492[/cite] |
| BH2 | 1.06 | 1.56 | 16.6 | [cite]10.14469/ch/189479[/cite] |
| BH2 | 1.53 | 1.03 | 17.6 | [cite]10.14469/ch/189492[/cite] |
| SiH3 | 1.48 | 1.04 | 18.8 | [cite]10.14469/ch/189481[/cite] |
| Z=S | 1.50 | 1.03 | 18.8 | [cite]10.14469/ch/193726[/cite] |
| BeF | 1.12 | 1.38 | 20.9 | [cite]10.14469/ch/189489[/cite] |
| BeF (TS) | 1.15 | 1.32 | 22.5 | [cite]10.14469/ch/193727[/cite] |
| BeF | 1.48 | 1.04 | 18.7 | [cite]10.14469/ch/189488[/cite] |
Another reality check, a search of crystal structures. DIST2 = OH, DIST1 = NH, for structures recorded below 140K, R < 0.05%, no errors, no disorder. The structure above is shown as a blue dot. They do tend to show asymmetry, but it is interesting how many such structures have emerged since our own 1989 report; the effect is not that rare any more.
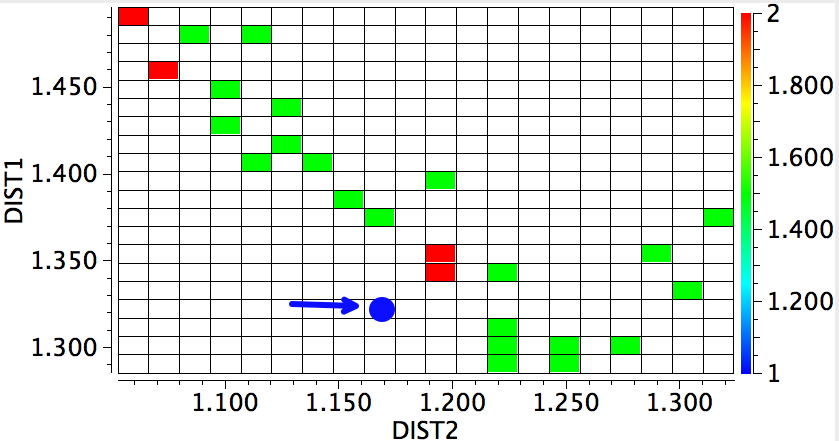
The above plot shows lots more systems that might be subjected to the sort of tuning above, and who knows one of them may even yield to experimental validation.
DOI: 10.14469/hpc/10731
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
Tags: energy, high chemical shifts, New Hampshire, unusual chemical shift