Andy Extance at the Chemistry World blog has picked up on a fascinating article[cite]10.1021/jz401578h[/cite] on the dimer of SF2. This molecule has three F atoms on one S, and only one on the other; FSSF3. But all four S-F bonds are of different length. Lindquist and Dunning claim that the minimum energy pathway to dissociation to two SF2 molecules does not involve breaking either the longest or the weakest SF bond. This was too much for me to resist investigating further!
Click for 3D
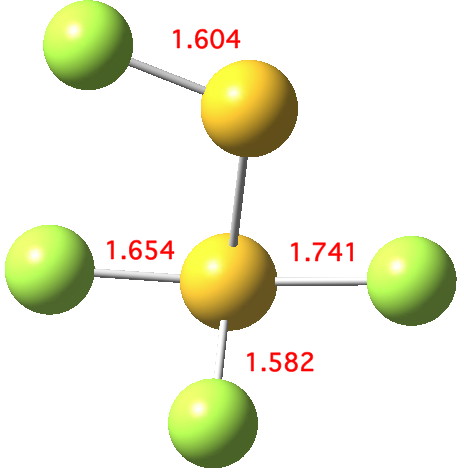
The computed ωB97XD/aug-cc-pVTZ geometry above[cite]10.6084/m9.figshare.791578[/cite] reveals the extent of the difference in bond lengths. What Lindquist and Dunning showed is that the two apparently longest (and implied weakest) SF bonds do not have the lowest bond dissociation energies, and offered an explanation using their methodology of coupled bond dyads obtained from GVB theory. But as a “transition state” person myself, I could not help but note that no such were described in their article. So I set out to look for one.
Firstly, I tried to find a transition state for [1,2] migration of the longest S-F bond (labelled 1.741Å above, axial at a trigonal bipyramidal S). Nope.‡ The one labelled 1.654Å seemed unlikely, so in desperation I tried the shortest S-F bond (1.582Å, equatorial at a trigonal bipyramidal S). Success! The computed IRC (ωB97XD/6-311G(d,p)[cite]10.6084/m9.figshare.797514[/cite] shows a surprise. The shortest S-F bond does indeed do a [1,2] migration, but it is accompanied in its travels by the longest S-F bond which also moves more or less in synchrony, although its motion is far less.
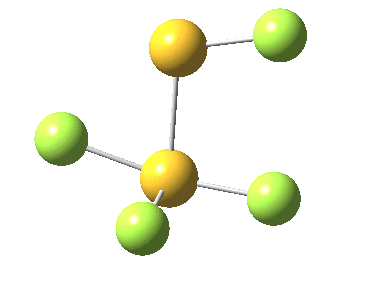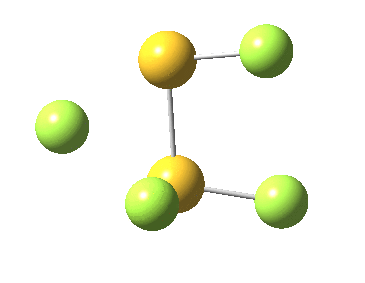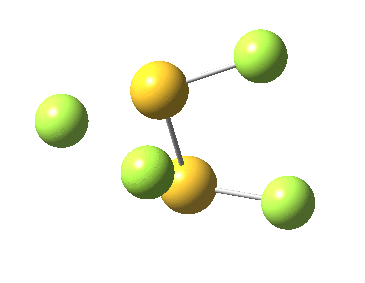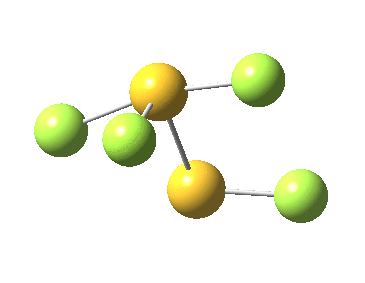
This transition state, it transpires is not on the pathway to dissociation, but is a double [1,2] migration (in this it is related to the coarctate mechanism, which involves two bonds breaking and two forming in a concurrent manner). It also has the feature associated with dyotropic rearrangements[cite]10.1039/C2CC33676F[/cite] that the central S-S bond is shorter at the transition state ((1.937Å) than for either reactant or product (2.073Å).
The barrier is > 60 kcal/mol (reduced only slightly by solvation[cite]10.6084/m9.figshare.798824[/cite]) which does rather tend to suggest that the formation of SF2 almost certainly involves homolytic dissociation and hence radicals, rather than a closed shell route found above.
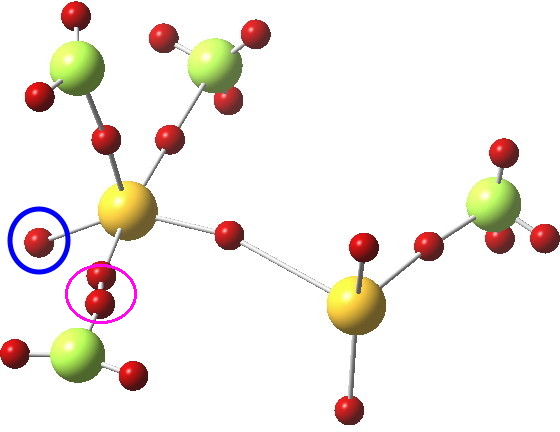
Not relevant to the previous topic, but related to the post on ClF3 is the ELF analysis; an attempt to identify where the electron basins (mono and disynaptic) are. The sulfur bearing the three fluorines has one lone “pair” (1.88e to be precise, ringed below), whilst the other S has two (2.25e each). The total integration for the 4-coordinate trigonal-bipyramidal S valence basins however (6.43e) clearly indicates no “octet expansion”.
There are lots lots more to enjoy about this molecule, do go read the Lindquist and Dunning article for a sense of this.
‡But I did find it eventually.
It is always fun to cross the cultural divide between organic and inorganic chemistry. Thus only an organic chemist would even attempt to push curly arrows for the (degenerate) reaction above. So here goes:
These are mad arrows by any standards, but I am following the rules I set out at this post. It might look as if there are four arrows and hence eight (formal) electrons involved, but in fact one pair of arrows (red) represents the same electron pair. It is supposed to show that the bond dyad for S-F is coupled to the bond dyad for S-S, and hence that at the transition state, the S-S bond is affected.
Another game one can play is to change elements for the adjacent one in the periodic table. Hence are the reactions of F4P-PF2 and F2Cl-Cl analogous to F3S-SF ?
The IRC for F4P-PF2 is shown below:
The IRC for F2Cl-Cl is again below:
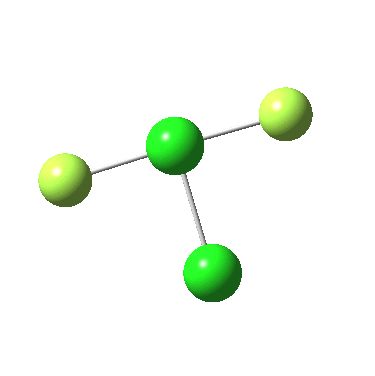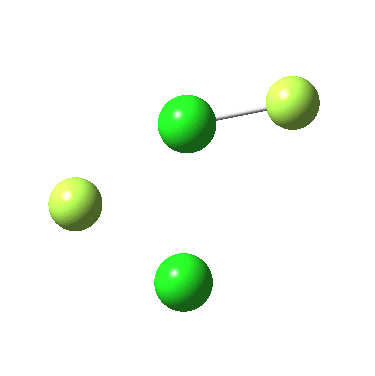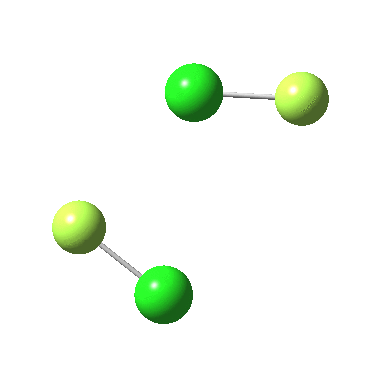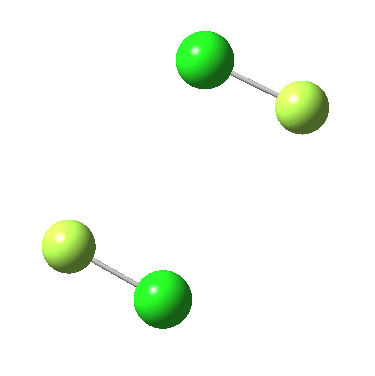
In both cases, they do what F3S-SF was loath to do; a reductive elimination to produce 2PF3 or 2FCl. So the behavour of F3S-SF is clearly different from that of the two elements to the left or right of sufur. As I noted before, weird!
In my post above, I reported finding a transition state for simultaneous migration of two F atoms from one S to the other, but that I had failed to find a transition state for migration of just one accompanied by cleavage of the S-S bond. In the comment above, I tried instead F4P-PF2 (a simpler system), and did indeed find such a transition state. So this has now allowed me to play a little game; using the transition state geometry of F4P-PF2 as a template, convert that to F3S-SF. There are in fact four ways of doing this conversion; one of them succeeded! The IRC for this new pathway is shown below
The activation barrier for the dimerisation of SF2 is about 25 kcal/mol, a normal closed shell thermal reaction barrier, and it is exothermic by about 12 kcal/mol, which is a known property of this molecule (the analogous reactions of the P and Cl isomers are endothermic).
The calculated (ωB97XD/6-311G(d,p) ) ΔG298 barriers are 28.7 for dimerisation and 34.3 kcal/mol for the retro-reaction.
But if you look carefully, the migrating F in fact ends up forming that longest S-F bond in F3S-SF (or, it is indeed that long bond that migrates for the reverse dissociation of F3S-SF to SF2). The structure of this transition state is quite similar to that reported a few years back; doi:10.1002/1099-0682(200109)2001:10<2543::AID-EJIC2543>3.0.CO;2-6 So a little bit of the weirdness has perhaps gone!
If you click on the top diagram in the post (the one captioned “Click for 3D”) you can view the calculated normal modes for the molecule. The one pre-selected has the value 201 cm-1, and it does seem to correspond to a [1,2] shift of the longest axial S-F bond. If you load the Jmol molecule, and right-click in the window and then select the top item in the pop-up menu (Model 4/14), you can then select other normal modes to view. None of these harmonic modes however quite correspond to the IRC shown above for the dissociation.
[…] Schleyer sent me an email about a pattern he had spotted, between my post on F3SSF and some work he and Michael Mauksch had done 13 years ago with the intriguing title […]