C2 (dicarbon) is certainly interesting from a theoretical point of view. Whether or not it can be described as having a quadruple bond has induced much passionate discussion[1],[2],[3],[4]. Its occurrence in space and in flames is also well-known. But does it have what might be called a conventional chemistry? Other highly reactive species (cyclobutadiene is a well-known example) can often be tamed by trapping as a ligand coordinated to a metal and so one might speculate upon how C2 responds to the proximity of a metal. As is noted here[2], dicarbon as a ligand has been known a long time as part of what is referred to as carbide chemistry. In this regard it is thought of as the di-anion, C22- (and isoelectronic therefore with dinitrogen). Thus calcium carbide, but in fact the degree to which the dicarbon can absorb electrons is thought to be wide (as judged by the resulting C-C bond length, see[2]). Here I take a look at just one metal carbide[5] that caught my eye (there are hundreds of others, many no doubt equally interesting!).
One first notices that the standard attempt at a representation above does not do it justice; a Lewis valence bond drawing (in which electrons are accounted by partitioning into bonds) it most certainly is not. Nine carbons and four osmiums have absorbed 21 electrons, donated (formally) from seven lanthanum atoms. But easily discerned is that of the nine carbons, four are dicarbon and five are mono carbon. It is worth exploring the immediate environment of each of these types. The monocarbon is in fact hexa-coordinated by two Os and four La, a form of carbon coordination that was only relatively recently identified.
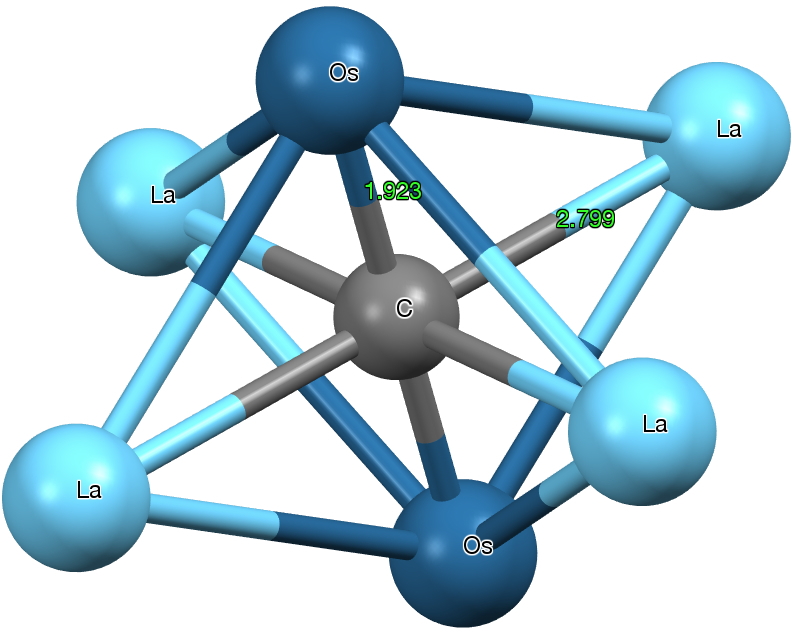
Click for 3D
But the dicarbon unit is if anything even stranger. The C-C bond length is ~1.316Å (a relatively long distance compared to many carbides) more or less commensurate with a double bond. The carbons are both end-on σ-coordinated and also triply π-coordinated. with one more metal coordinating in a manner somewhat in-between these two modes. One carbon is 5-coordinate, the other 6-coordinate. The Os-C bond length has a relatively short value of 1.93Å (the sum of the double bond covalent radii for Os and C is 1.83, the single bond radii 2.04), and so it might be tempting to represent it as Os=C=C.
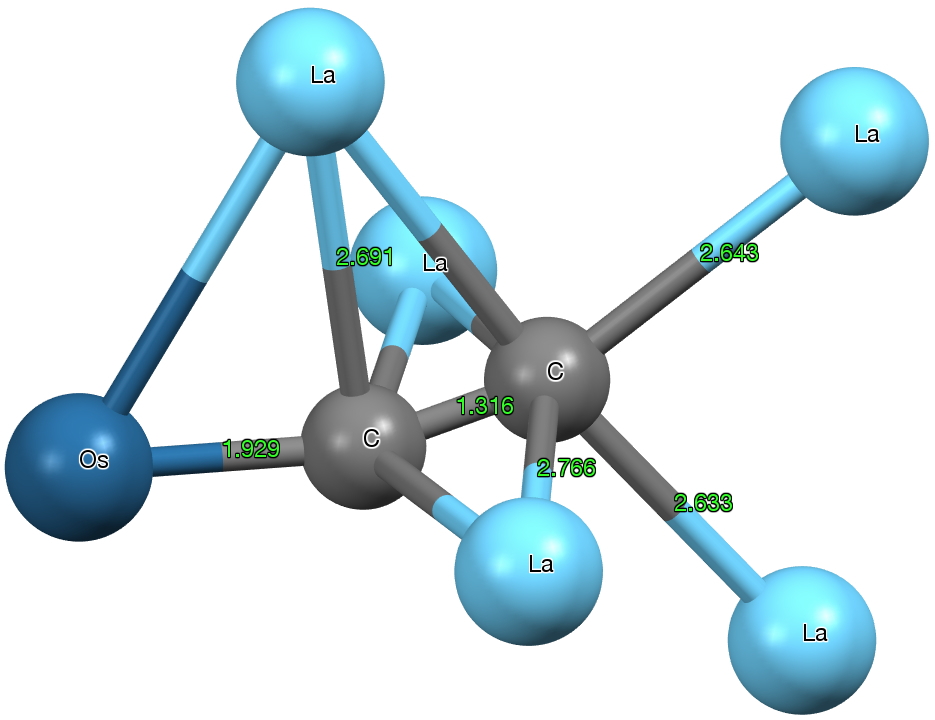
Click for 3D
This one example reminds us that even an element such as carbon, where one might imagine the bonding environments would be well-known, can still reveal unusual behaviours. Taking a look at the histogram below, which indicates C-C lengths in Metal-CC-Metal complexes (where the carbon coordination is restricted to 2) indicates the diversity of behaviour possible with this simple little ligand.
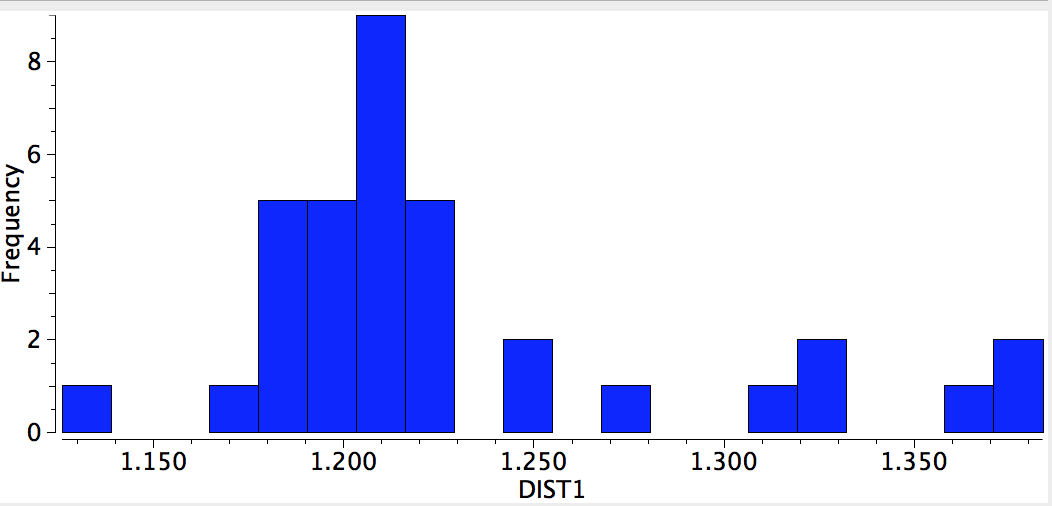
References
- S. Shaik, D. Danovich, W. Wu, P. Su, H.S. Rzepa, and P.C. Hiberty, "Quadruple bonding in C2 and analogous eight-valence electron species", Nature Chemistry, vol. 4, pp. 195-200, 2012. https://doi.org/10.1038/nchem.1263
- S. Shaik, H.S. Rzepa, and R. Hoffmann, "One Molecule, Two Atoms, Three Views, Four Bonds?", Angewandte Chemie International Edition, vol. 52, pp. 3020-3033, 2013. https://doi.org/10.1002/anie.201208206
- G. Frenking, and M. Hermann, "Critical Comments on “One Molecule, Two Atoms, Three Views, Four Bonds?”", Angewandte Chemie International Edition, vol. 52, pp. 5922-5925, 2013. https://doi.org/10.1002/anie.201301485
- D. Danovich, S. Shaik, H.S. Rzepa, and R. Hoffmann, "A Response to the Critical Comments on “One Molecule, Two Atoms, Three Views, Four Bonds?”", Angewandte Chemie International Edition, vol. 52, pp. 5926-5928, 2013. https://doi.org/10.1002/anie.201302350
- E. Dashjav, Y. Prots, G. Kreiner, W. Schnelle, F.R. Wagner, and R. Kniep, "Chemical bonding analysis and properties of La7Os4C9—A new structure type containing C- and C2-units as Os-coordinating ligands", Journal of Solid State Chemistry, vol. 181, pp. 3121-3130, 2008. https://doi.org/10.1016/j.jssc.2008.08.005
Tags: metal, metal coordinating, Os-C
Octahedral hexacoodination carbon was “well established” much earlier in CLi6, neutral, radical cation, and dication in J. Am Chem. Soc. 1982, 104, 4275; 1983, 105, 5930 and verified experimentally in Nature, 1992, 355, 432.
Cf. Schmidbaur, Angew. Chem. Int. Ed. 1988, 27, 1544 for C(AuX)6 [HSR: its CCDC Refcode is SAKSEC] and also nitrogenase, with its C(Fe)6 moiety [HSR: for 1974 crystal structure of a hexacoordinate carbon, see 10.1039/DT9740002410, Refcode MACHFE]
Thanks Paul for those valuable citations. Tetrahedral carbon coordination was famously established in 1874, but 5 and 6-coordinate carbon had to wait ~100+ years to become established. I suspect in some carboranes the coordination is even higher!
At the end of my post, I showed a search of some 50 M-CC-M systems, revealing the diversity of bond lengths that are shown. Here I attach two further plots. A further variable is added, the M-CC angle, and the search is also repeated for M-NN-M. Notice how for the M-CC-M system, almost all the examples are linear, whereas for the (possibly isoelectronic) M-NN-M systems they cluster into highly bent and linear. Amongst the linear cluster, again a diversity of bond lengths is observed.
Oddly, the (again possibly isoelectronic) CN(-) anion shows much less distance diversity, clustering at around 1.15Å, very large variation about the M-N-C angle, and almost none about the M-C-N angle.
Paul in his comment gave a short history of the discovery of 5- and 6-coordinate carbon. I thought I would do a simple scan of the CCDC with the following search definition: a single carbon, specified to have 5, 6, 7 or 8 bonded atoms (along with R factor < 0.05, no disorder, no errors). The results were as follows: 5: 2061 6: 1796 7: 19 8: 4 Which of course begs the question: how is a bonded atom defined? One would have to look up the criteria used by CCDC to index its structures, but we should be aware that a bond is probably not defined in any Lewis sense of shared electrons. Most probably its done on the basis of distances, and the hits above do not carry much semantics regarding the type of bonding associated with eg an 8-coordinate carbon.
Well, given the statistics in my previous comment, it seemed trivial to add a similar survey, this time with N as the coordinated atom
5: 136
6: 25
7: 0
8: 0
With the caveat as above that the definition of a coordination/bond to the central atoms is rather arbitrary (there is no simple way of computing this, even from a high quality wavefunction), the difference between C and N is striking.
What about the other direction in the periodic table, B:
5. 988
6: 2791
7: 224
8: 16
9: 2
11: 1
I again remind that these numbers may be an artefact of the way that CCDC define a “bond”, but one may presume at least they are consistent between B, C and N. And of course one is assuming that the distribution of reported crystal structures is not biased against any one of these elements.
Here is another exploration of coordination using the CCDC, this time the coordination number of hydrogen, H.
3: 277
4: 17
5: 5
6: 5 (a number of which are H surrounded octahedrally by metals)
7: 0.
(for a search with R < 5%, no disorder, no errors).